对不同大小的数据进行规范化

1、创建一些样本数据，其中y的值比x的值大几个数量级。假设x和y有不同的单位。

x = rand(1,500)/100; 

y = 2.*(rand(1,500)-0.5).*90; 

z = (x.*1e2).^2; 

2、使用示例数据构建查询点网格。在网格上插入样本数据并绘制结果。

X = linspace(min(x),max(x),25); 

Y = linspace(min(y),max(y),25); 

[xq, yq] = meshgrid(X,Y); 

zq = griddata(x,y,z,xq,yq); 

plot3(x,y,z,'mo')

hold on

mesh(xq,yq,zq)

xlabel('x')

ylabel('y')

hold off

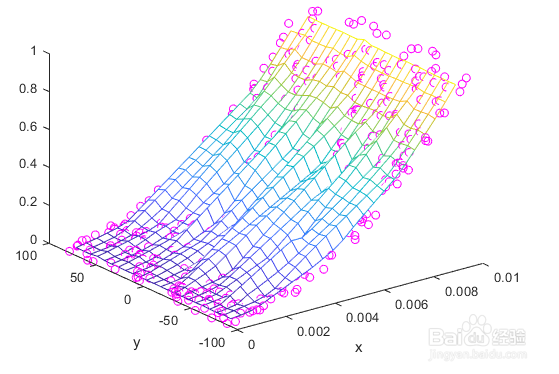
3、griddata产生的结果不是很平滑，似乎是有噪声的。自变量的不同尺度导致了这一点，因为一个变量的大小的一个小变化可能导致另一个变量的大小的一个大得多的变化。

由于x和y有不同的单位，将它们归一化使它们有相似的大小应该有助于产生更好的结果。使用标准偏差对采样点进行归一化，使用griddata重新生成插值。

4、% Normalize Sample Points

x = (x-mean(x))/std(x);

y = (y-mean(y))/std(y);

% Regenerate Grid 

X = linspace(min(x),max(x),25); 

Y = linspace(min(y),max(y),25); 

[xq, yq] = meshgrid(X,Y); 

% Interpolate and Plot

zq = griddata(x,y,z,xq,yq);

plot3(x,y,z,'mo')

hold on

mesh(xq,yq,zq)

5、在这种情况下，规格化采样点允许griddata计算更平滑的解决方案。