线段树建树、区间修改以及区间求和(C++写法)
1、附上题目
题目描述
给你一个包含N个整数的数列:A1, A2, ... , AN。 你需要来完成两种操作:1、对于一个区间的每个数字加上某个数值;2、询问一个区间的数字之和。
输入
1行:两个数字N和Q。1 ≤ N,Q ≤ 100000。2行:包含N个整数,初始值为A1, A2, ... , AN。-1000000000 ≤ Ai ≤ 1000000000。接下来Q行,每行表示一个操作。"C a b c" 表示 Aa, Aa+1, ... , Ab中每个数,加上c。 -10000 ≤ c ≤ 10000。"Q a b" 表示询问 Aa, Aa+1, ... , Ab的和。
输出
你需要输出每个查询操作的结果,每个回答一行。

2、建树并将树上节点定为初始值,这个过程比较简单,主要是深搜,代码如下
struct tree{
int left,right,value;
}s[maxn];
void build(int i,int left,int right)
{
s[i].left=left;
s[i].right=right;
if(left==right)
{
s[i].value=a[left];//a是这个节点的权值
return ;
}
build(i*2,left,(left+right)/2);
build(i*2+1,(left+right)/2+1,right);
s[i].value=s[i*2].value+s[i*2+1].value;
}


3、第二,就是求和了,这里用的方法是每个点加一个add值,代表这个节点的所有叶节点的值都要加上add,而每次往下深搜时,将此节点的add值更新到两个叶子节点上,并将原来这个节点的权值更新。这点学到后面非常重要。
void que(int i,int lef,int rig)
{
if(s[i].add!=0)
{
s[i].value+=s[i].add*(s[i].right-s[i].left+1);
s[2*i].add+=s[i].add;
s[2*i+1].add+=s[i].add;
s[i].add=0;
}
if(s[i].left>=lef && s[i].right<=rig)
{
sum+=s[i].value;
return ;
}
int kk=i*2;
if(s[kk].right>=lef)que(kk,lef,rig);
if(s[kk+1].left<=rig)que(kk+1,lef,rig);//不断往下深搜
}

4、第三,区间更新,如果当前搜索到的节点被包含在你要修改的区间中,就将此节点的add值更新。
void addtree(int i,int val,int lef,int rig)
{
if(s[i].left>=lef && s[i].right<=rig)
{
s[i].add+=val;
return ;
}
if(lef>=s[i].left && rig<=s[i].right)s[i].value+=val*(rig-lef+1);
else s[i].value+=val*(min(abs(s[i].right-lef+1),abs(rig-s[i].left+1)));
if(s[i].add!=0)
{
s[i].value+=(s[i].right-s[i].left+1)*s[i].add;
s[2*i].add+=s[i].add;
s[2*i+1].add+=s[i].add;s[i].add=0;
}
int kk=2*i;
if(s[kk].right>=lef)addtree(kk,val,lef,rig);
if(s[kk+1].left<=rig)addtree(kk+1,val,lef,rig);
}

5、最后附上源代码
#include<iostream>
#include<cstdio>
#include<cmath>
using namespace std;
struct tree{
int left,right;
long long value,add;
}s[1000001];
//int fa[100001];
int n,q;
long long sum,a[100001];
void build(int i,int left,int right)
{
s[i].left=left;
s[i].right=right;
if(left==right)
{
s[i].value=a[left];
return ;
}
build(i*2,left,(left+right)/2);
build(i*2+1,(left+right)/2+1,right);
s[i].value=s[i*2].value+s[i*2+1].value;
}
void que(int i,int lef,int rig){
if(s[i].add!=0)
{
s[i].value+=s[i].add*(s[i].right-s[i].left+1);
s[2*i].add+=s[i].add;s[2*i+1].add+=s[i].add;s[i].add=0;
//s[2*i].value+=(s[2*i].right-s[2*i].left+1)*s[2*i].add;
//s[2*i+1].value+=(s[2*i+1].right-s[2*i+1].left+1)*s[2*i+1].add;
}
if(s[i].left>=lef && s[i].right<=rig)
{
sum+=s[i].value;return ;
}
int kk=i*2;
if(s[kk].right>=lef)que(kk,lef,rig);
if(s[kk+1].left<=rig)que(kk+1,lef,rig);
}
void addtree(int i,int val,int lef,int rig){
if(s[i].left>=lef && s[i].right<=rig)
{
s[i].add+=val;
//s[i].value=s[i].value+s[i].add*(s[i].right-s[i].left+1);
return ;
}
if(lef>=s[i].left && rig<=s[i].right)s[i].value+=val*(rig-lef+1);
else s[i].value+=val*(min(abs(s[i].right-lef+1),abs(rig-s[i].left+1)));
if(s[i].add!=0)
{
s[i].value+=(s[i].right-s[i].left+1)*s[i].add;
s[2*i].add+=s[i].add;s[2*i+1].add+=s[i].add;s[i].add=0;
//s[2*i].value+=(s[2*i].right-s[2*i].left+1)*s[2*i].add;
//s[2*i+1].value+=(s[2*i+1].right-s[2*i+1].left+1)*s[2*i+1].add;
}
int kk=2*i;
if(s[kk].right>=lef)addtree(kk,val,lef,rig);
if(s[kk+1].left<=rig)addtree(kk+1,val,lef,rig);
}
int main()
{
scanf("%d%d",&n,&q);
for(int i=1;i<=n;i++)scanf("%lld",&a[i]);
build(1,1,n);
for(int i=1;i<=q;i++)
{
char k;
cin>>k;
if(k=='C')
{
int d;
int b,c;
scanf("%d%d%d",&b,&c,&d);
addtree(1,d,b,c);
}
if(k=='Q')
{
int b,c;
scanf("%d%d",&b,&c);
sum=0;
que(1,b,c);
printf("%lld\n",sum);
}
}
}

1、Q 表示询问一段区间内所有数的和,C表示把一段区间内所有数加上一个值( 详见方法的第一步)
样例输入
10 4
1 2 3 4 5 6 7 8 9 10
Q 4 4
Q 1 10
Q 2 4
C 3 6 3
样例输出
4 55 9
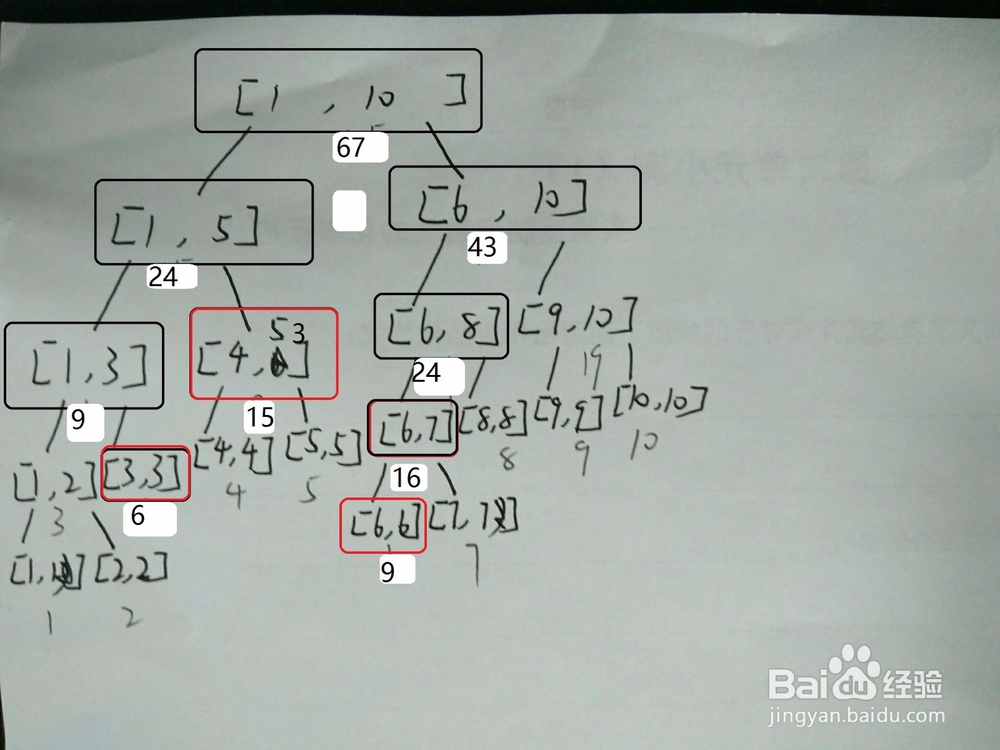
2、首先先建树,并将每个子节点的值更新,然后往上更新



3、首先是查找4-4的和,从根节点往下查找

4、接下来查找1-10的和,同样从根节点往下找

5、接下来查找2-4的和,最后的答案为三个红框框出的节点的值之和
6、接着在3-6的节点各加3,先从根节点往下搜,搜到所有红框框住的节点,此时add值就有用了,【4,5】节点中写的3即为此节点的add值,如果后面还有查找的话,就将父节点的add值加到两个子节点上,加给子节点不是平均分配,而是 子节点的add值都加上父节点的add值,并把父节点的add值归零。