2^x-3^y=45的渐近线的绘制

1、用Mathematica求不定方程的正整数解：

FindInstance[2^x-3^y==45,{x,y},Integers,3]

结果：

The methods available to FindInstance are insufficient to find the request edinstances or prove they do not exist

2、然后用网络画板画图。

3、通过观察，发现图像应该有两条渐近线。

于是，在网络画板里面作图：

y=k*x

其中，k是变量，取值范围是0到1，代表直线y=k*x的斜率。

4、拖动变量尺k，可以发现，当k≈0.63的时候，直线与曲线贴合了。

5、用Mathematica解方程：

f[x_]:=(Solve[2^x-3^y==45 ,y]//Values)[[1,1]]//FullSimplify //Normal

6、计算f[x]/x的极限：

k=Limit[f[x]/x,x->Infinity]

而k=Log[2]/Log[3]≈0.63092975357。

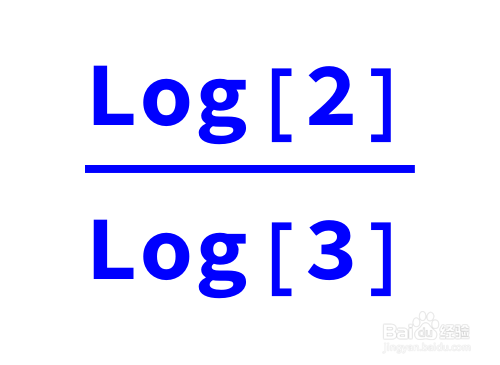
7、所以，曲线的一条渐近线是：

y=(Log[2]/Log[3])*x

8、另一条渐近线的计算方法：

g[y_]:=FullSimplify[Re[(Solve[2^x-3^y==45 ,x]//Values)[[1,1]]],

           Refine[Element[y,Reals]]]//Normal

k=Limit[g[y],y->-Infinity]

k=Log[45]/Log[2]

  ≈5.4918530963296747107777973173850231933844602084095

所以，第二条渐近线是：

x=Log[45]/Log[2]