勾股定理的应用

1、一. 认真审题，考虑分类思想，注意两种情况

  例1. 已知中，BC=5，AC=12。求AB的长。

分析：受勾股数组的影响，同学们往往认为本题只有一解，即AB=13。但本题没有明确提出哪条边是斜边，所以应就AC为斜边或直角边这两种情况加以讨论。

解：当AC为斜边时：

当AC为直角边，AB为斜边时：

2、例2. 已知△ABC中，AB=40，AC=30，BC边上的高为24。求△ABC的面积。

分析：考虑到△ABC的形状不确定，应分BC边上的高在△ABC内和△ABC外两种情况讨论。

解：当BC边上的高在△ABC内时，如图1所示，AD⊥BC。

当BC边上的高在△ABC外时，如图2所示，AD⊥BC。

3、二. 结合一次函数、轴对称性质，灵活解有关勾股定理的综合题

  例3. 已知A（1，3），B（4，2），点P为x轴上一点。求使AP+BP的值最小时点P的坐标和AP+BP的最小值。

分析：A，B两点分布在x轴的同侧，点P在x轴上，要使AP+BP最小，必须将A，B两点转化为在x轴的异侧，且使两点到P的距离不变。这样使所求问题转化为两点间距离最短的问题。我们可通过对点A或点B作关于x轴的对称点，然后构造直角三角形，利用勾股定理解决问题。先由已知两点坐标求一次函数解析式，然后求一次函数图象与x轴交点即可求出P点坐标。

解：作点B关于x轴的对称点

设过A，的直线为（k，b为常数，）

解之，得

当y=0时，，即直线与x轴交于点

∵此时的值为最小

∴当AP+BP取最小值时，点P的坐标为

过A作AC//y轴，过作轴，交点为C

，且

∴AP+BP的最小值为

4、练一练：

  1. 等腰三角形周长为900px，一边长为250px，则底边上的高为多少厘米？

  2. 已知等腰三角形的一边长为10，面积为30，求等腰三角形的周长。

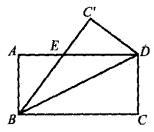
  3. 如图4，将矩形ABCD沿着对角线BD折叠，使点C落在处，交AD于E，AD=8，AB=4，求△BED的面积。

5、4. 如图5，一个正方体小盒，一只小虫要沿盒的表面从A点爬到B点，请结合你学过的知识，给小虫指明一条最短路线。

6、参考答案：

  1. 300px或150px

点拨：分腰为250px和底为250px两种情况。

  2. 或或

点拨：分底边长为10和腰长为10进行讨论，当腰长为10时再分锐角三角形和钝角三角形进行讨论。

  3. 10

  4. 略

1、例1. 已知中，BC=5，AC=12。求AB的长。

2、例2. 已知△ABC中，AB=40，AC=30，BC边上的高为24。求△ABC的面积。

3、例3. 已知A（1，3），B（4，2），点P为x轴上一点。求使AP+BP的值最小时点P的坐标和AP+BP的最小值。

4、练一练

5、练一练

6、参考答案