MATLAB在单自由度振动的应用

1、 问题：

一单自由度系统，固有频率wn=1，初始条件，y0=1，v0=5，系统的阻尼大小可变，讨论系统在过阻尼、小阻尼和无阻尼情况下的自由振动。

2、分析1：

当系统的阻尼为0，称为无阻尼，此时系统的振动响应如下图公式所示：

3、分析2：

当系统的阻尼比介于0~1之间，称为小阻尼，此时系统的振动响应如下图公式所示：

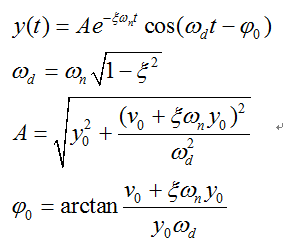
4、分析3：

当系统的阻尼比大于1，称为过阻尼，此时系统的振动响应如下图公式所示：

5、MATLAB计算

假设：过阻尼时阻尼比为1.5，过阻尼时阻尼比为0.5，无阻尼时阻尼比为0，则MATLAB计算命令如下所示：

clear

t=0:0.01:20;

wn=5;y0=1;v0=5;

%%阻尼比znb=0时，计算无阻尼响应

znb=0;

A1=sqrt(y0^2+(v0/wn)^2);

phi1=atan(v0/(y0*wn));

y1=A1*cos(wn*t-phi1);

subplot(3,1,1);

plot(t,y1);

ylabel('{\ity}_1');

grid on

%%阻尼比znb=0.1时，计算小阻尼响应

znb=0.1;

wd=wn*sqrt(1-znb^2);

A2=sqrt(y0^2+(v0+znb*wn*y0)^2/wn^2);

phi2=atan(v0+znb*wn*y0)/(y0*wd);

y2=A2*exp(-znb*wn*t)*diag(cos(wd*t-phi2));%使用diag函数生成对角阵满足矩阵乘法运算。

subplot(3,1,2);

plot(t,y2);

ylabel('{\ity}_2');

grid on

%%阻尼比znb=1.5时，计算过阻尼响应

znb=1.5;

r1=(-znb+sqrt(znb^2-1))*wn;

r2=(-znb-sqrt(znb^2-1))*wn;

A=(v0-r2*y0)/(r1-r2);

B=(v0-r1*y0)/(r2-r1);

y3=A*exp(r1*t)+B*exp(r2*t);

subplot(3,1,3);

plot(t,y3);

ylabel('{\ity}_3');

xlabel('{\itt}');

grid on