【python】基于numpy的矩阵奇异值分解

1、假设a是一个m*n的矩阵，对应的奇异值分解是：

a=u.v.w

那么，u是一个m*m的矩阵，v是一个m*n的对角矩阵（下面将着重介绍这一点），w是一个n*n的矩阵。

比如：

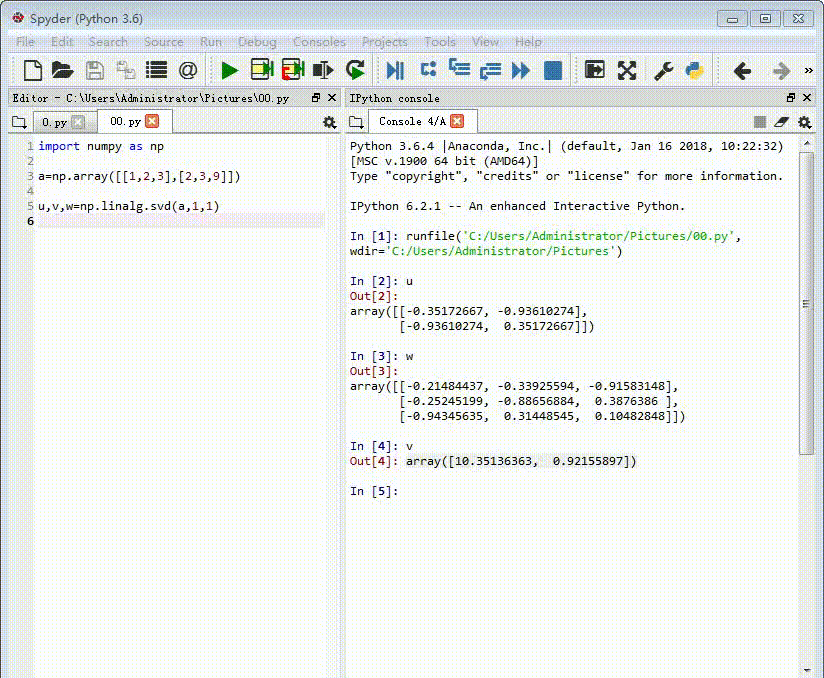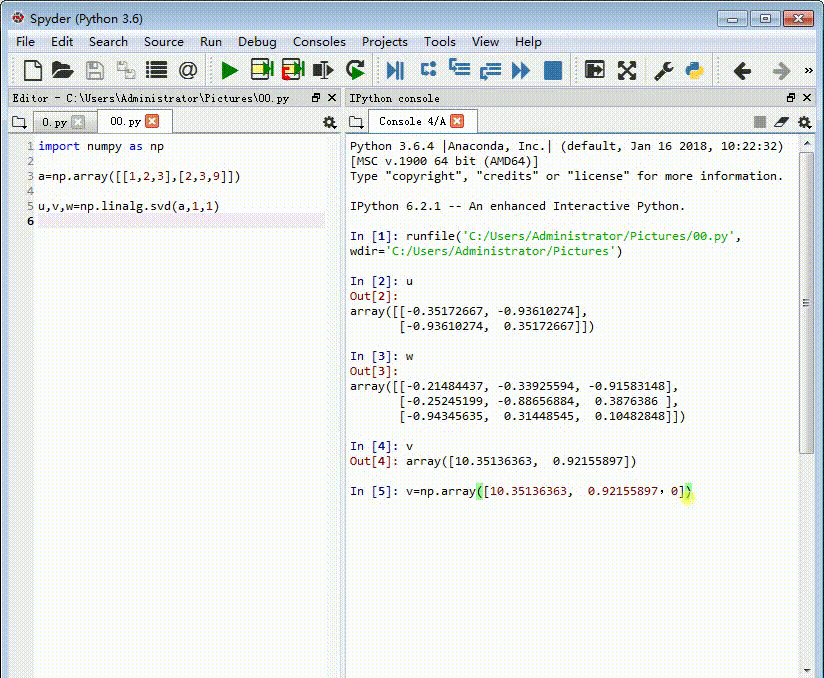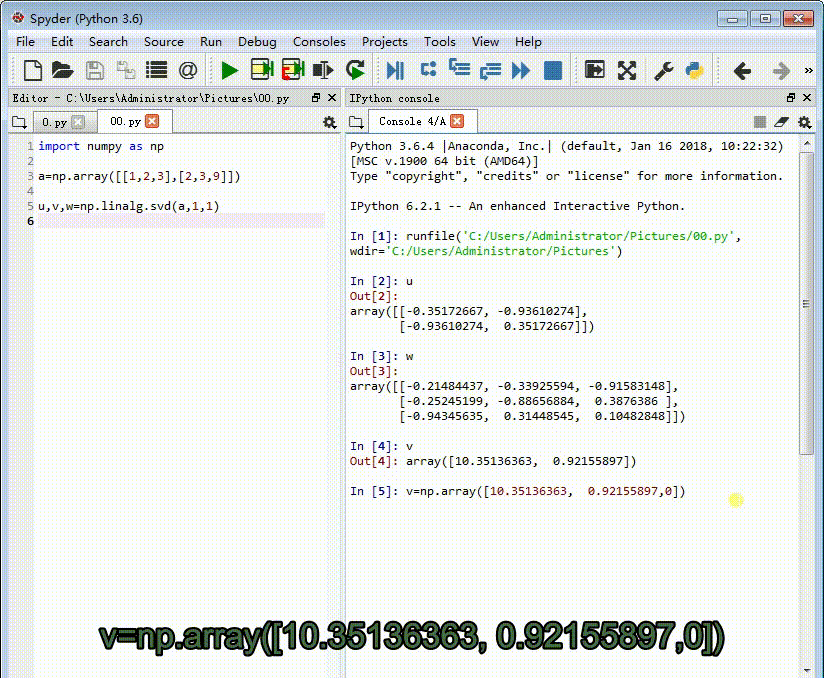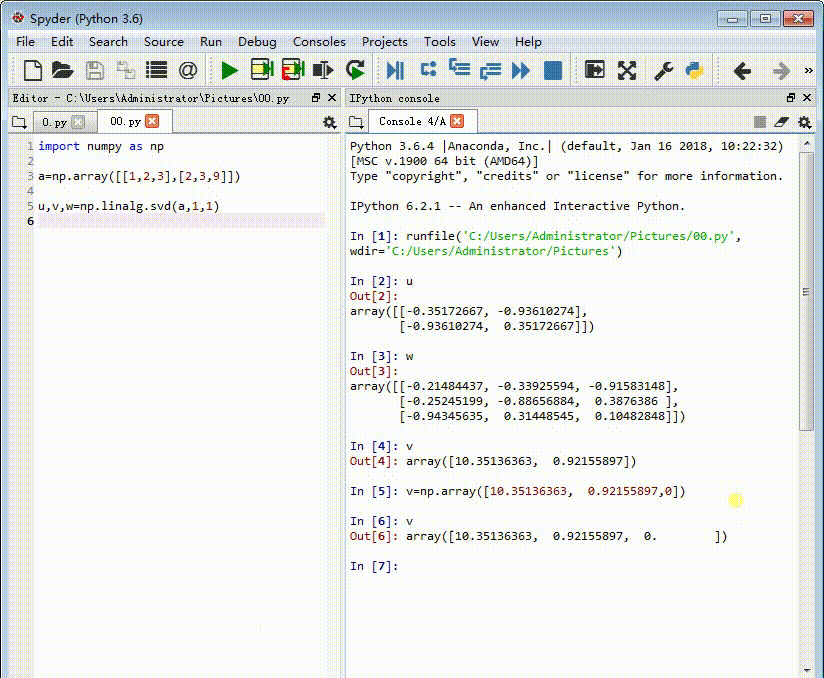
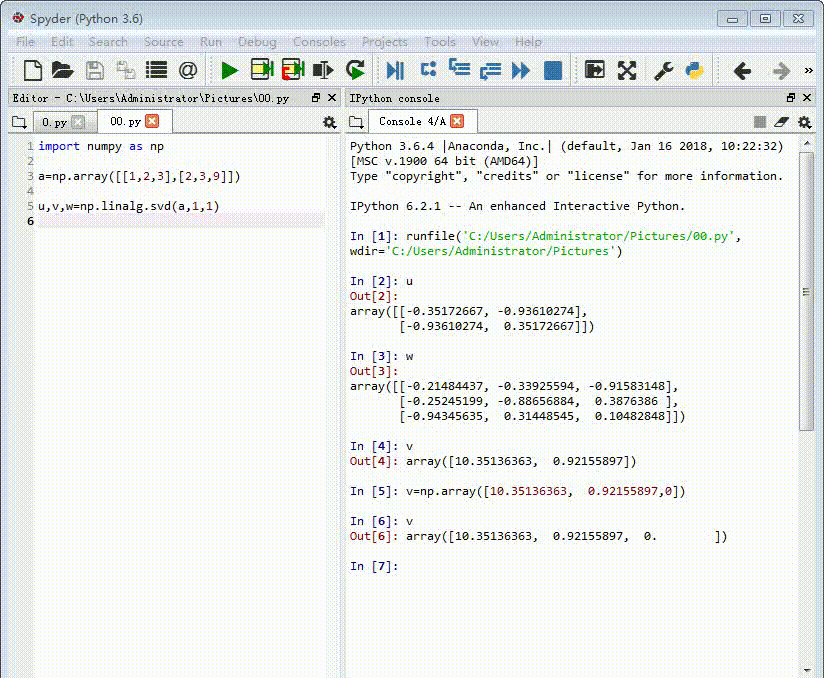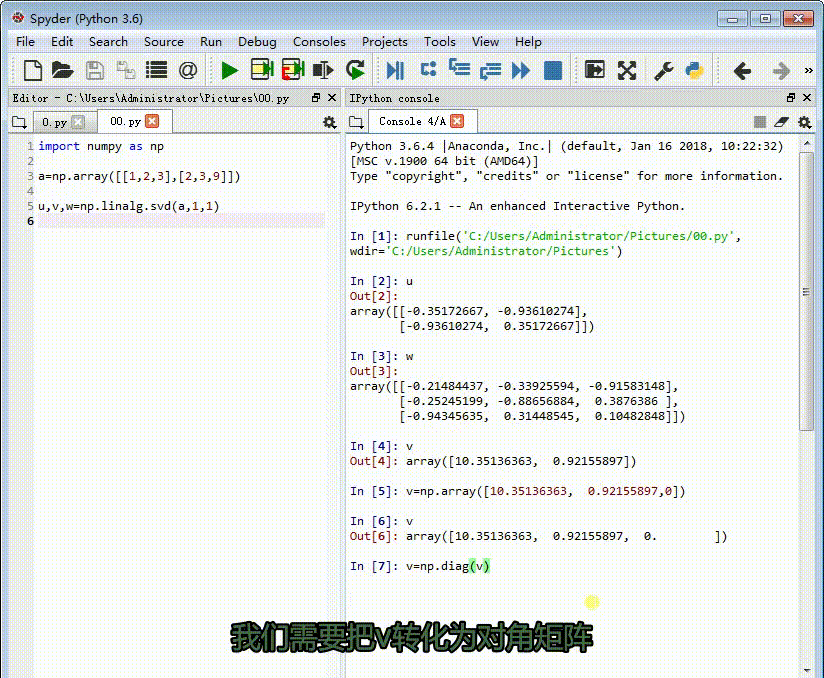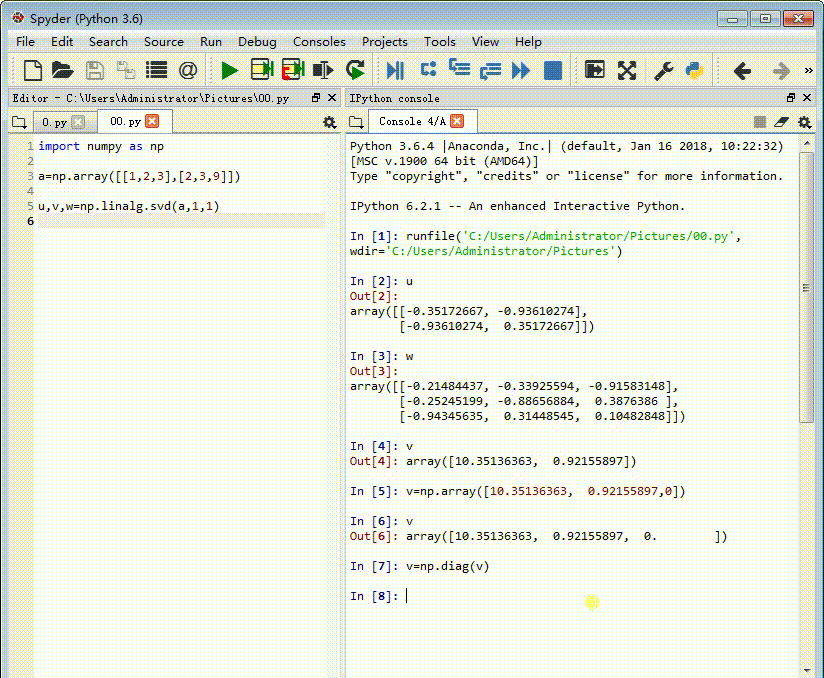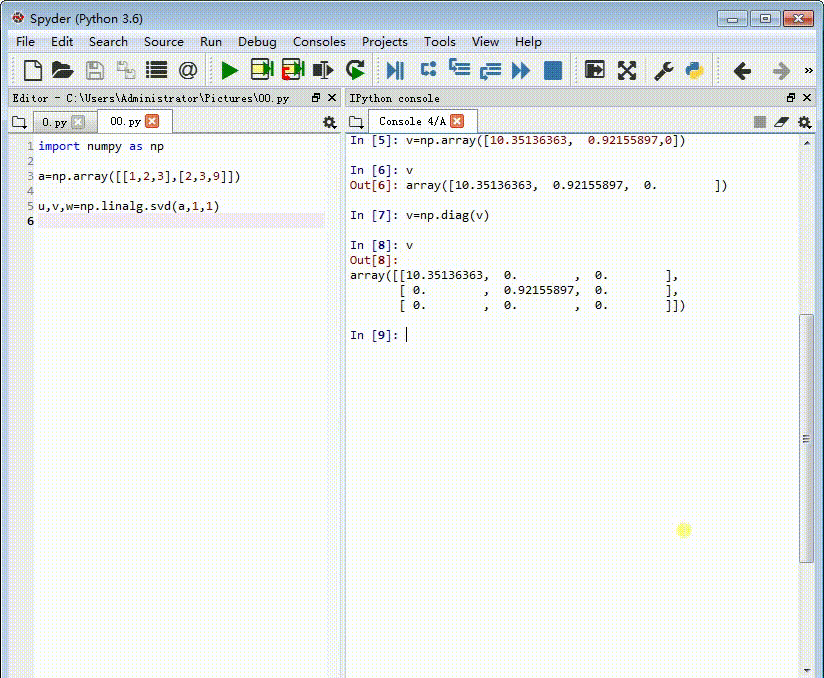
a=np.array([[1,2,3],[2,3,9]])

u,v,w=np.linalg.svd(a,1,1)

u是一个2*2的矩阵，w是一个3*3的矩阵，v比较特殊。

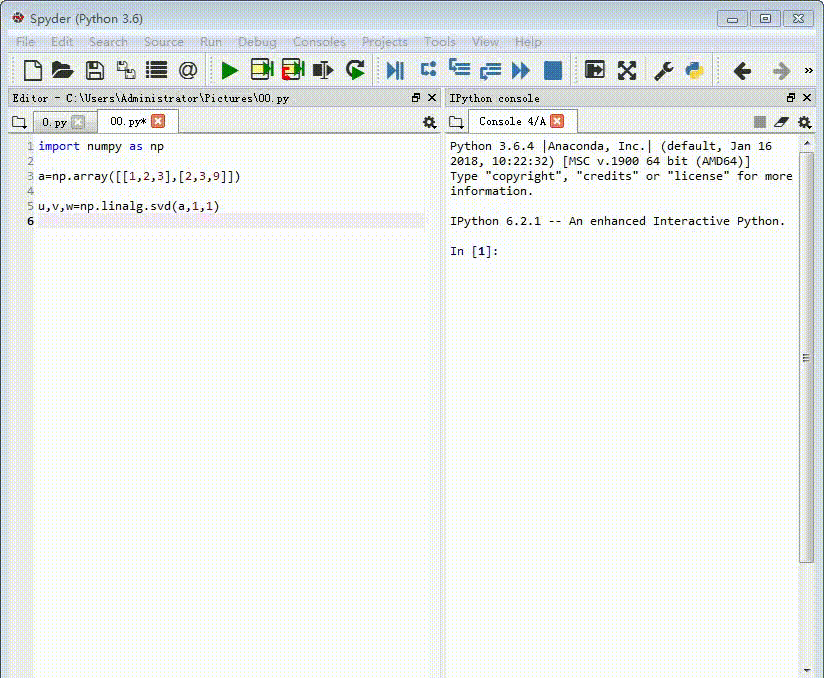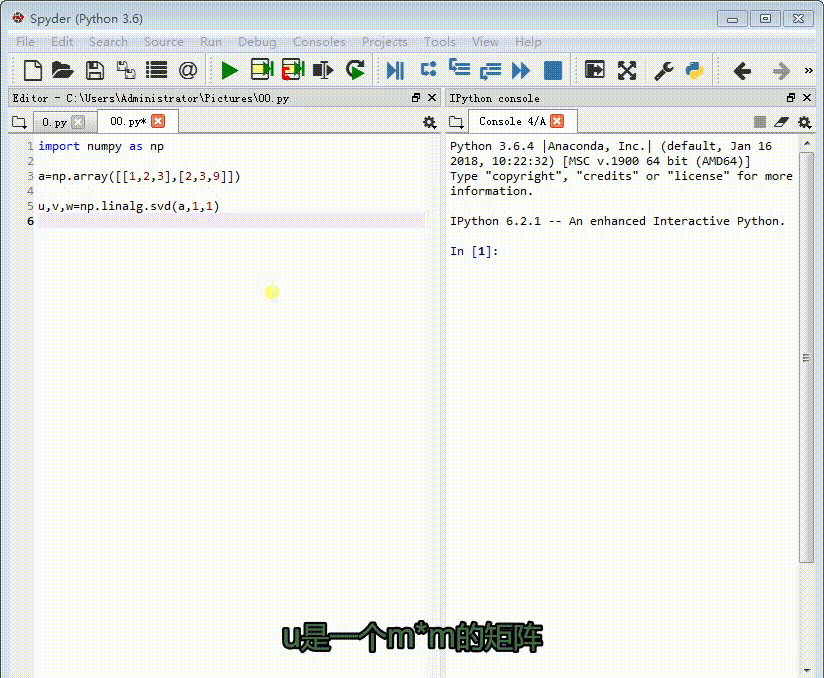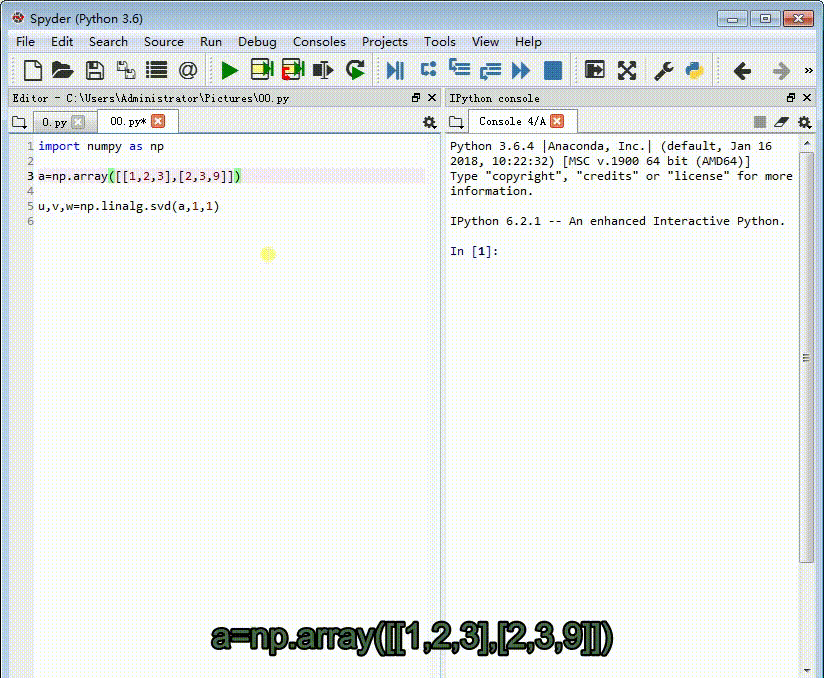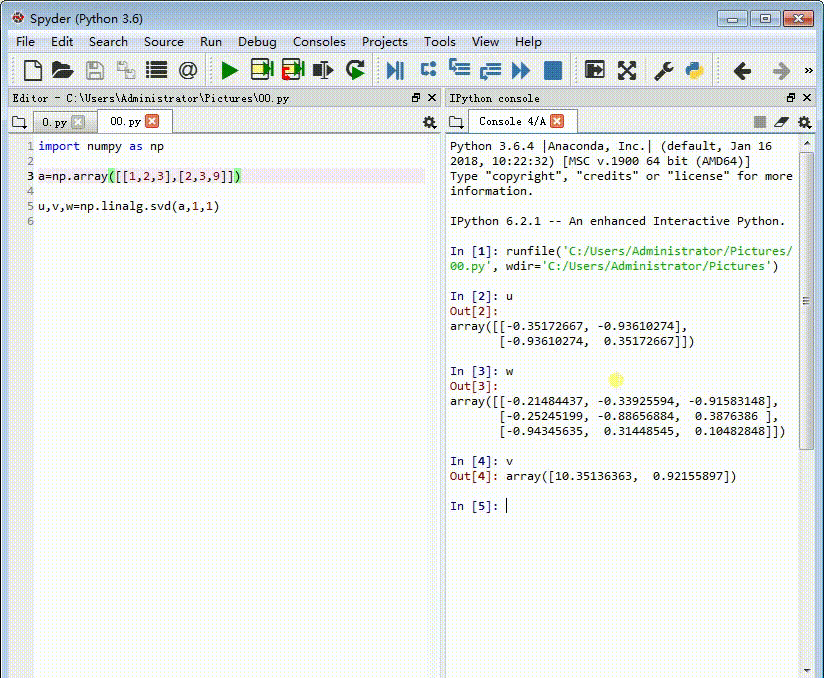
2、这里得到的v只有两个元素，其实还有第三个元素，由于很接近与0，所以被忽略了。

我需要把它补全。

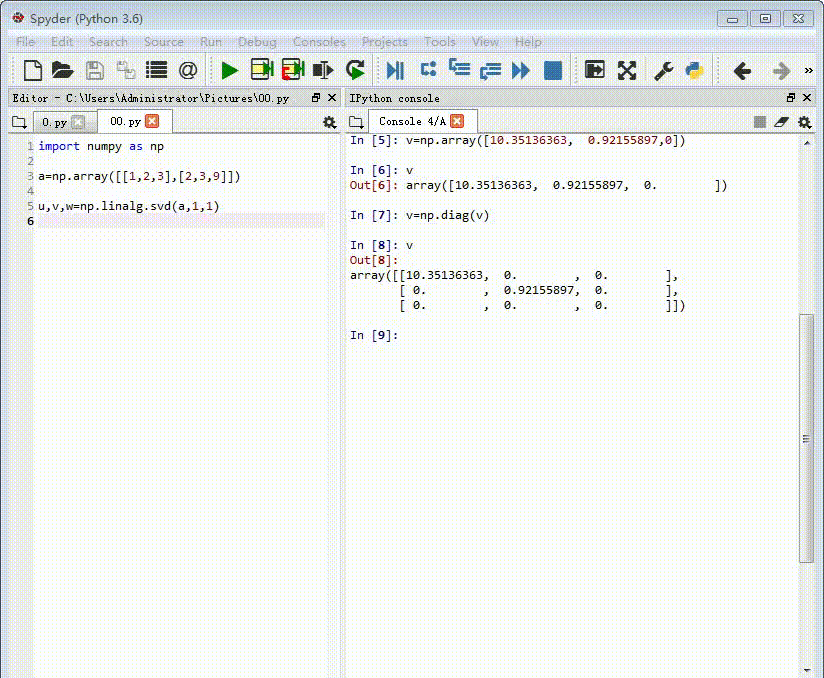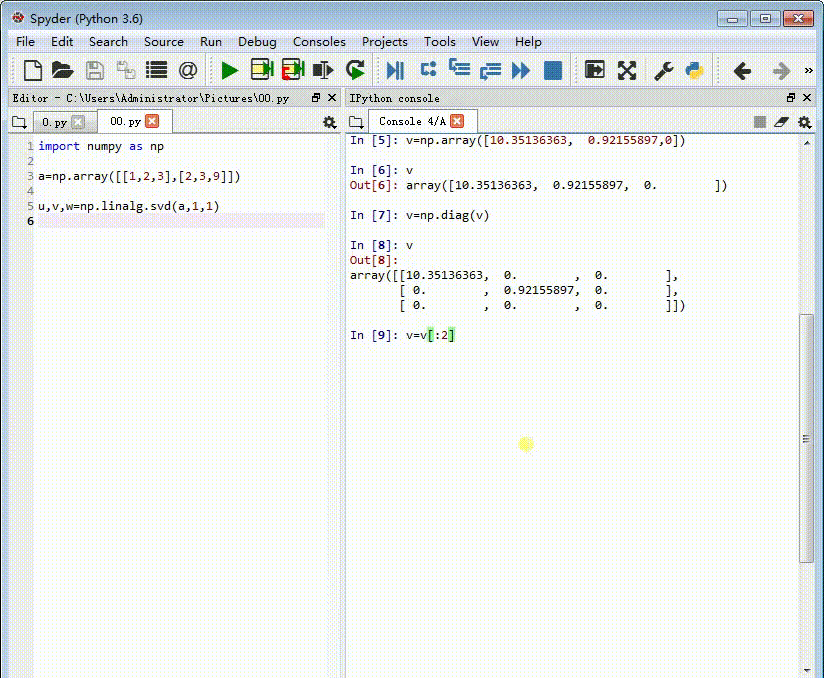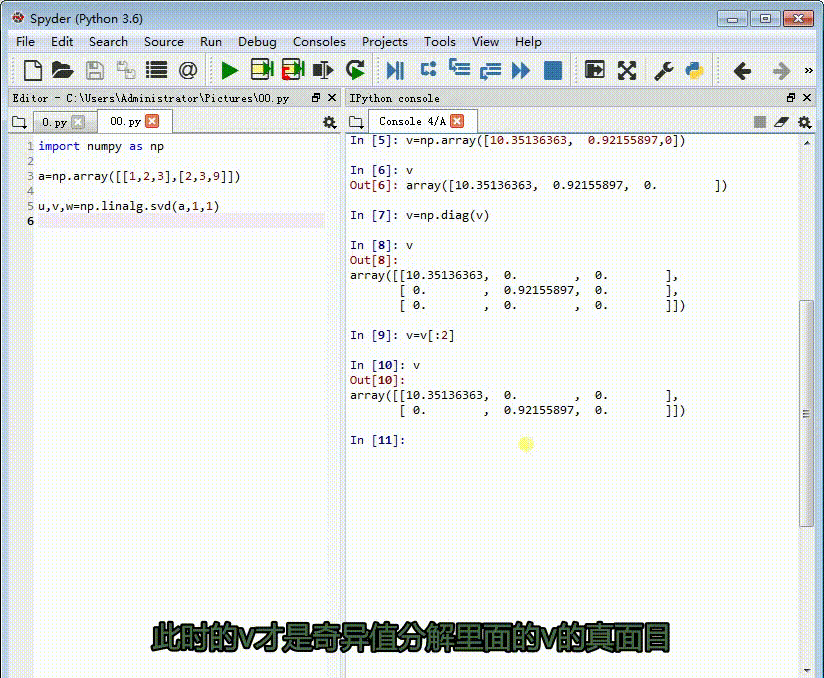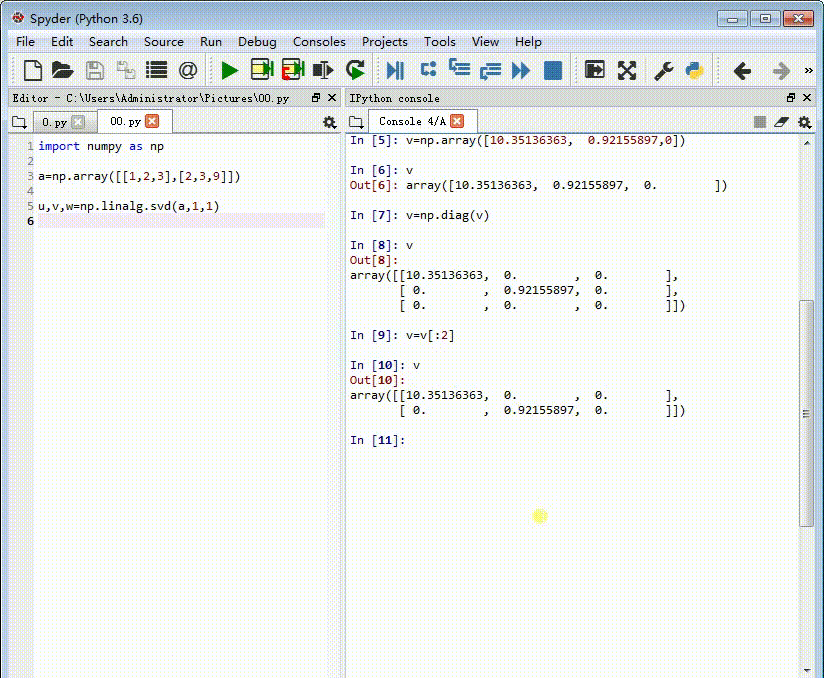
v=np.array([10.35136363,  0.92155897,0])

3、此时的v实际上是一个对角矩阵的三个元素，我们需要把v转化为对角矩阵：

v=np.diag(v)

4、注意到第三行全部都是0，需要把第三行去掉：

v=v[:2]

此时的v才是奇异值分解里面的v的真面目。

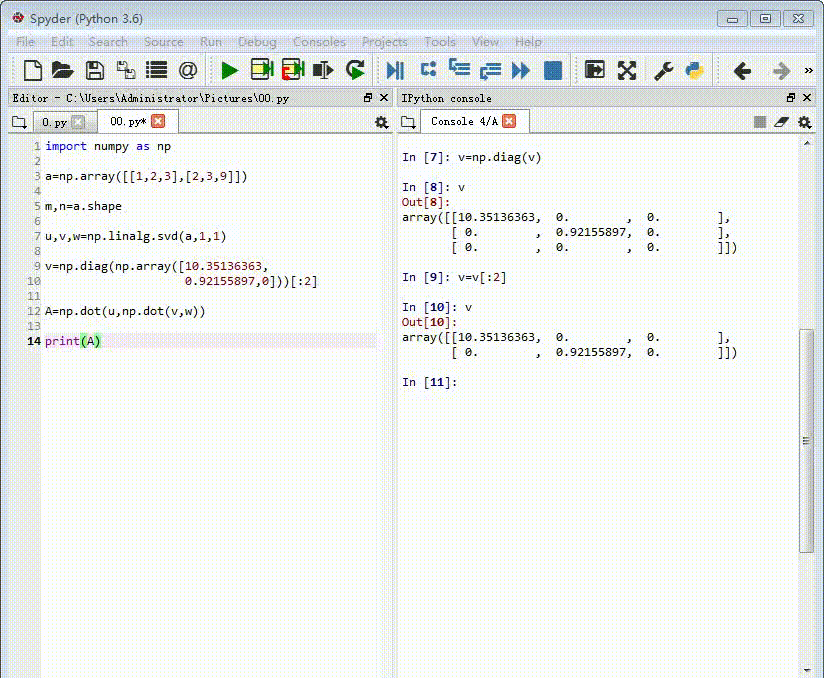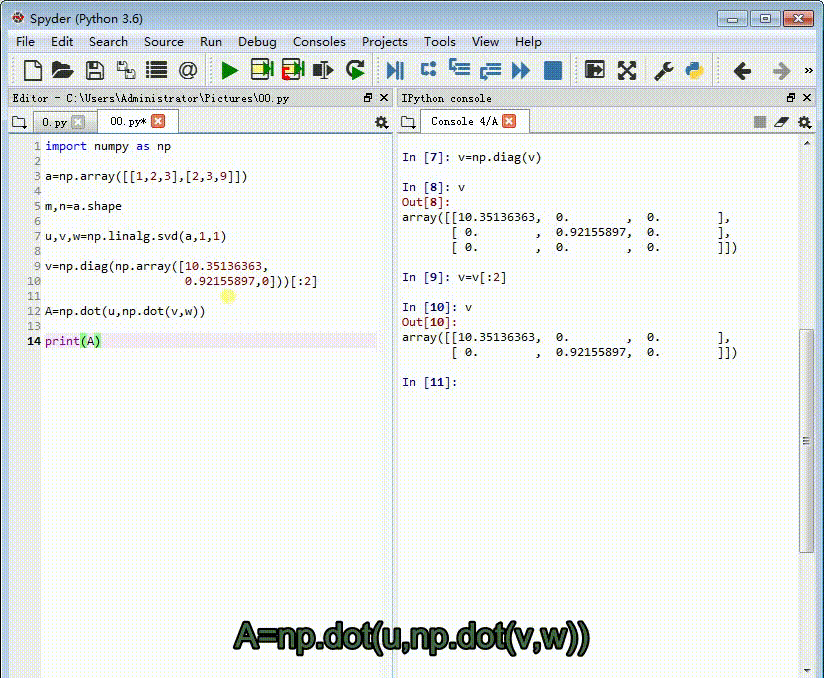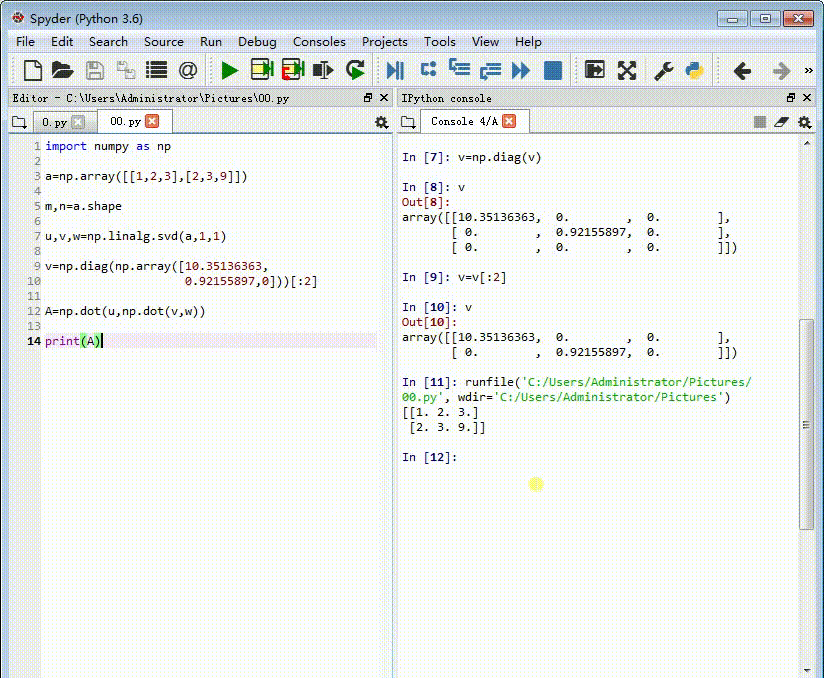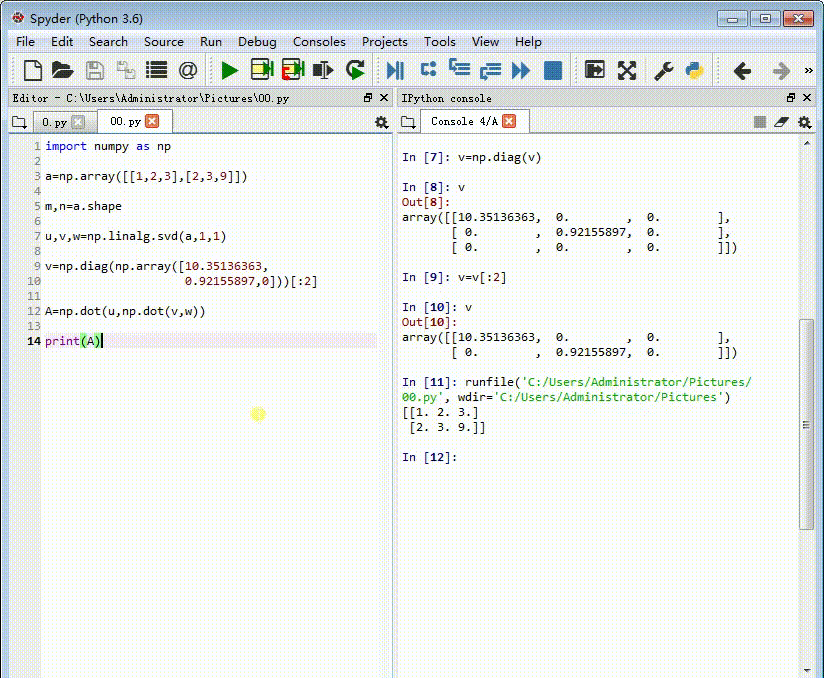
5、检验一下：

A=np.dot(u,np.dot(v,w))

6、再来看看另一个例子。