电路布线问题(动态规划)
1、最优子结构性质
记N(i,j) = {t|(t, π(i)) ∈ Nets,t ≤ i, π(t) ≤ j }. N(i,j)的最大不相交子集为MNS(i,j)。Size(i,j)=|MNS(i,j)|。
2、当i = 1时
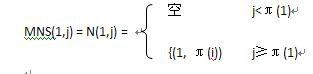
3、当i >1时,
① j <π(i)。此时,(i,π(i)) 不属于N(i,j)。故在这种情况下,N(i,j) = N(i-1,j),从而Size(i,j)=Size(i-1,j).
② j ≥π(i)。此时,若(i, π(i))∈MNS(i,j),则对任意(t,π(i))∈MNS(i,j)有t < i且π(t)< π(i);否则,(t, π(t))与(i,π(i))相交。在这种情况下MNS(i,j)-{(i, π(i))}是N(i-1, π(i)-1)的最大不相交子集。否则,子集MNS(i-1, π(i)-1)∪{(i, π(i))}包含于N(i,j)是比MNS(i,j)更大的N(i,j)的不相交子集。这与MNS(i,j)的定义相矛盾。
若(i, π(i))不属于MNS(i,j),则对任意(t, π(t))∈MNS(i,j),有t<i。从而MNS(i,j)包含于N(i-1,j),因此,Size(i,j)≤Size(i-1,j).
另一方面,MNS(i-1,j)包含于N(i,j),故又有Size(i,j) ≥Size(i-1,j),从而Size(i,j)= Size(i-1,j).
4、递归计算最优值
经以上后分,可电路布线问题的最优值为Size(n,n)。由该问题的最优子结构性质可知:

5、根据上面递归式可以得到二维表:
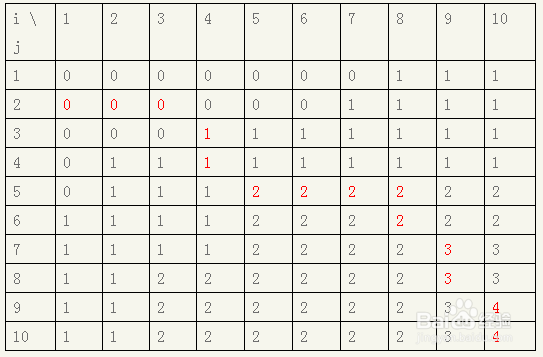
6、红色标明的就是算法选择的路径(向上优先,也可以用向左优先,答案都是四个,但值会有一点不同)。在斜角值改变时可以取得所求的子集。
即 9->10,7->9,5->5,3->4
1、/*
* 计算最优值
* 输入参数C[]: 接线方式
* 输入参数n : 接线柱数
* 输入参数size: 二维表数组
*/
void mnset(int C[],int n,int *size)
{
int i,j;
// 当i = 1时
for(j = 0;j<C[1];j++)
{
size[n+j] = 0;
}
for(j = C[1];j <= n;j++)
{
size[n+j] =1;
}
// 当i >=2时
for ( i = 2; i< n; i ++)
{
for ( j = 0; j<C[i] ; j++)
{
size[i*n+j] = size[(i-1)*n+j] ;
}
for ( j = C[i] ; j <= n ; j++)
{
size[i*n+j] = max(size[(i-1)*n+j],size[(i-1)*n+C[i]-1]+1);
}
}
size[n*n] = max(size[(n-1)*n],size[(n-1)*n+C[n-1]-1]+1);
}
2、/*
* 构造最优值
* 输入参数C: 接线方式
* 输入参数size: 二维表数组
* 输入参数n : 接线柱数
* 输入参数Net: 最大子集数组
* 输入参数m: 最大子集数
*/
void traceBack(int C[], int *size, int n, int Net[], int &m)
{
int i,j = n;
m = 0;
for (i = n;i>1;i--)
{
if (size[i*(n+1)+j] != size[(i-1)*(n+1)+j])
{
Net[m++] = i;
j = C[i] - 1;
}
}
if (j >= C[1])
{
Net[m++] = 1;
}
}
3、测试代码
int main()
{
int n; // 接线数目
int num; // 最大子集数
int *l; // 接线方式
int *p; // 子集数
int *size; // 二维表数组
cout << "请输入电路的接线柱数:";
cin >> n;
// 动态创建热线方式数组
l = new int[n+1];
// 动态创建子集数组
p = new int[n+1];
// 临时动态创建二维数组
int **temp;
temp=new int*[n+1];
for(int i=0;i<n+1;i++)
{
temp[i]=new int[i+1];
}
// 将二维表二维数组以一维指针赋给size
size = &temp[0][0];
cout << "请依次输入连接数:" << endl;
for(int i=1;i<=n;i++)
cin>>l[i];
// 调用计算最优值函数
mnset(l,n+1,size);
// 调用构造最优值函数
traceBack(l,size,n,p,num);
// 打印子集数
cout << "最大不想交子集数:" << num << endl << endl;
//打印出子集
cout << "最大不想交子集" << endl;
for(int i = 0;i<num;i++)
cout << p[i] << " --> "<< l[p[i]] << endl;
system("pause");
return 0;
}