高中数学三种方法证明最小值

1、首先，由题意可以联想到基本不等式：a²+b²≥2ab，b²+c²≥2bc，a²+c²≥2ac。

将上式相加会得到新条件：a²+b²+c²≥ab+bc+ac。

即：

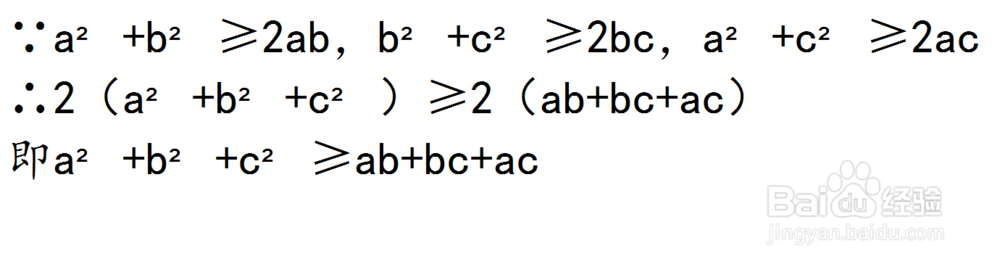
2、那么，看到a²+b²+c²这样的式子，我们显然会想到完全平方公式——（a+b+c）²=a²+b²+c²+2ab+2bc+2ac。

既然知道上式中的一部分大于等于某个值，那么，我们就可以联立二式，得到（a+b+c）²≥3ab+3bc+3ac。

又因为a+b+c=1，那么ab+bc+ac≤1/3。

即：

3、从上一步可以看出，我们要证明的式子中的a²+b²+c²，必然会和ab+bc+ac有关，所以对此式进行处理：-2（ab+bc+ac）≥-2/3。

那么问题就很简单了，只要把（a+b+c）²展开并代入条件就可以得证了。

即：

1、首先由已知条件a+b+c=1想到要引入新参数t，写出t符合的条件（t1+t2+t3=0）后，把要证的a²+b²+c²用含t的式子表示出来：a²+b²+c²=（a+t1）²+（b+t2）²+（c+t3）²

即：

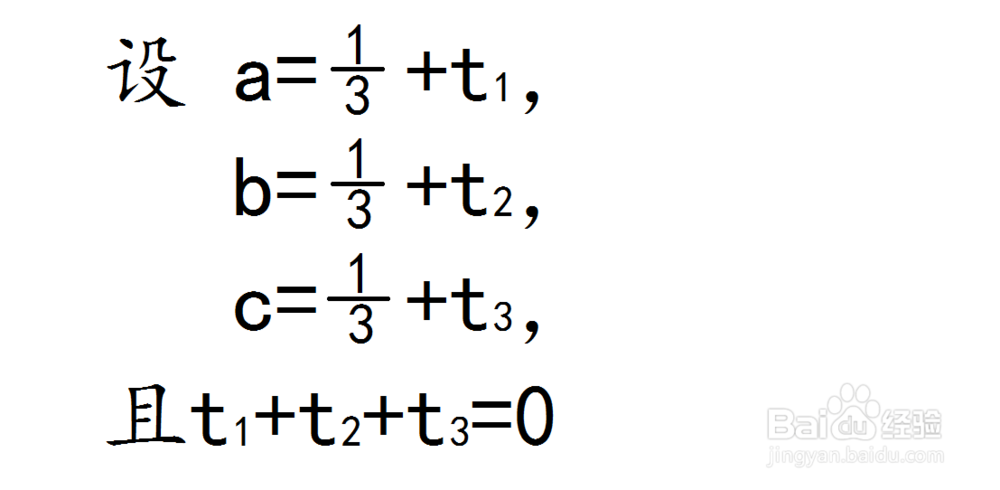
2、然后根据完全平方公式展开含t的式子，就可以得证。

即：

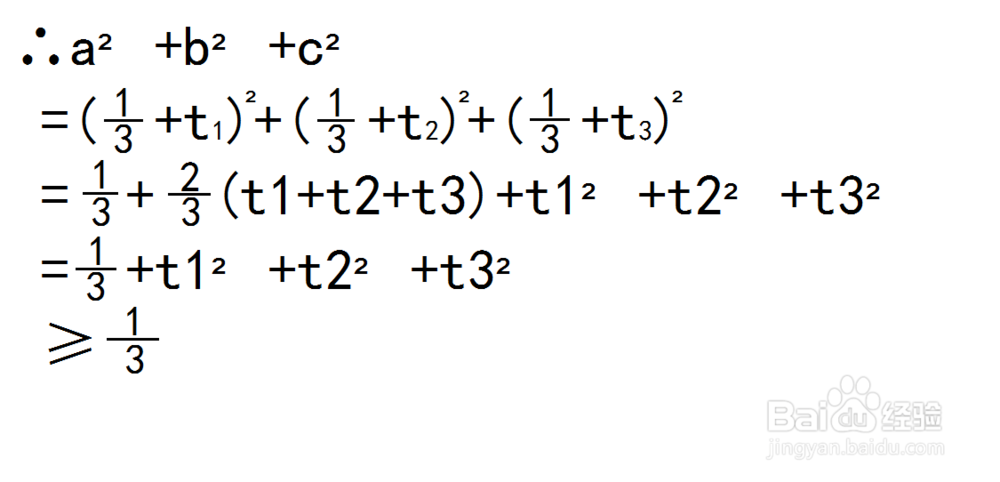
3、注：

分析t1+t2+t3=0可知：

t1、t2、t3均为0时，三数平方和最小，为0；

另外的三种情况下t1、t2、t3的平方和都不为0而是正数——1个为0、另外两个互为相反数；1个为负数、另外2个为正数；1个为正数、另外2个为负数。

综上：t1²+t2²+t3²≥0