【微分几何】怎么绘制正方形环面？

1、先绘制一个正方形环面。

正方形的极坐标方程可以是Cos[π/4] Sec[π/4 - Mod[h + t,  π/2]]，其中h是任意实数，而t是参数。

这个正方形沿着x轴平移，再绕z轴旋转，就得到一个环面。

下图是h=0的情形。

2、h=π/4的时候，效果如下。

3、把正方形环面切开一个口子，一段扭转45°，再对接回去，就得到一个莫比乌斯环面，这个图形只有一个外表面，只有一条外棱。

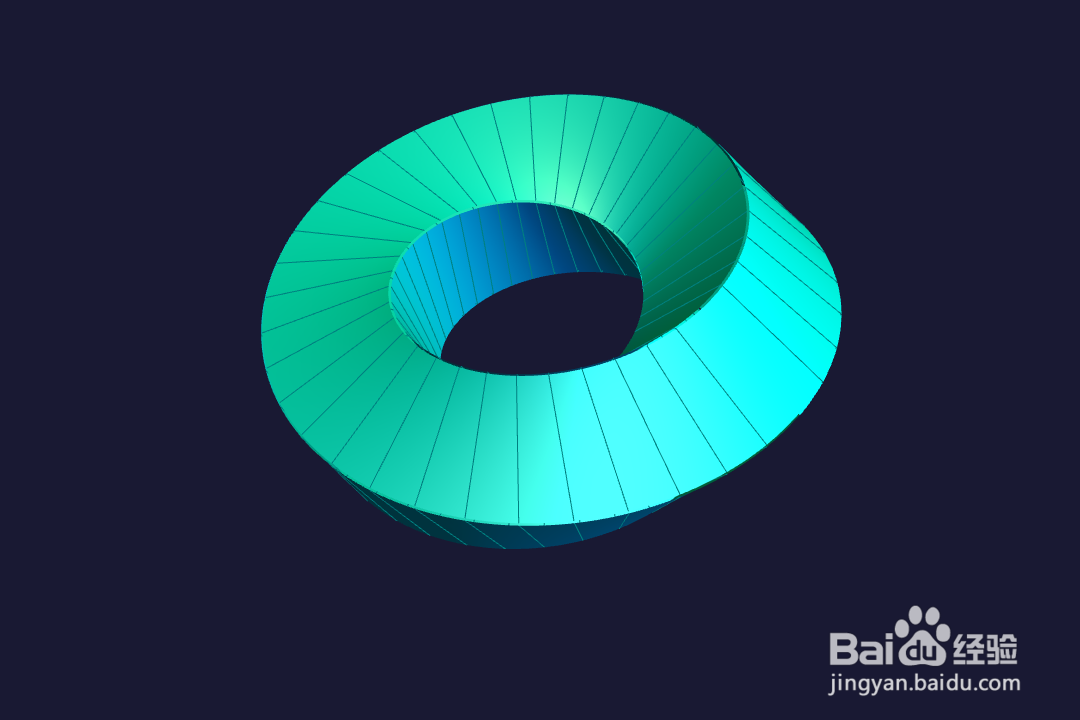
4、为了验证这一点，准备一个透明的图片。

你可以用思维在这个曲面上跑一圈，验证一下。

5、扭转90°，得到的莫比乌斯环有两个面，两条外棱。

6、扭转135°，得到的是一个外表面、一个外棱的莫比乌斯环，但与步骤4里面的不一样。

7、扭转180°的效果如下。

8、扭转360°和270°的效果如下。