使用Python理解和实践机器学习一元线性回归算法
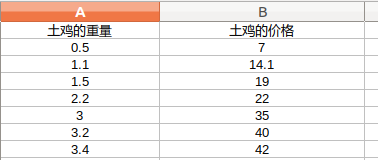
1、训练数据的准备:该数据集只有x和y两列值,X变量代表土ji的重量,y变量代表土ji的出售价格
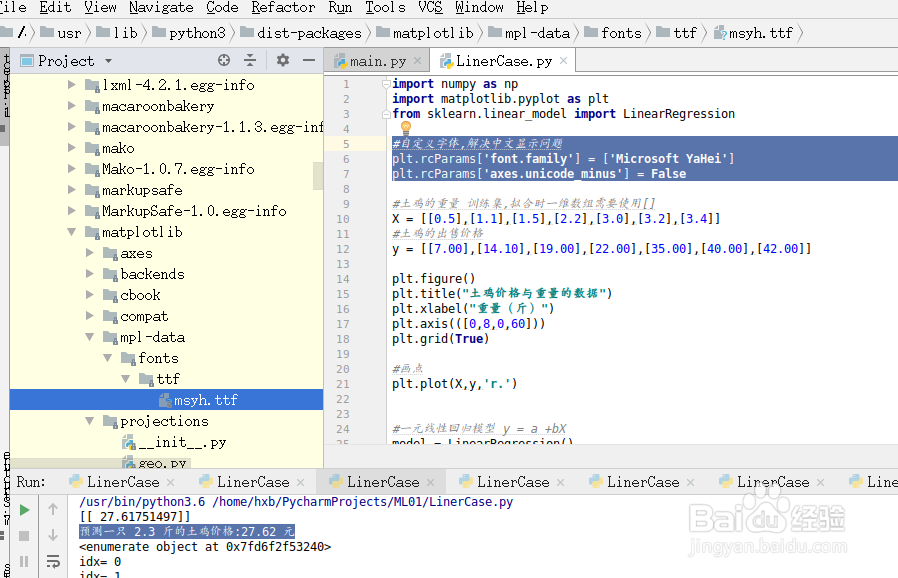
2、Python中Matplotlib中文库支持环境准备,需要先将微软雅黑字体文件复制到Matplotlib ttf字体目录下,具体方法参考以下的经验连接:
#自定义字体,解决中文显示问题
plt.rcParams['font.family'] = ['Microsoft YaHei']
plt.rcParams['axes.unicode_minus'] = False
1、了解一元线性回归模型: y = a + b* X, 代表一条直线
其中参数X为已知的自变量,这里X代表土ji的重量
y表示求解预测的目标变量,代表土ji的价格
a为模型系数
b为模型系数
通过训练数据求解模型系数a和b就是我们接下来要做的事情

2、求解模型系数b,采用如下公式
b = cov(x,y)/var(x)
其中cov(x,y)代表x,y的协方差值, var(x)代表x的方差值
我们可以直接采用numpy的方差和协方差函数求解
cov(x,y) = numpy.cov(x,y)
var(X) = numpy.var(X)
具体代码如下:
X = [0.5,1.1,1.5,2.2,3.0,3.2,3.4]
var_X = np.var(X,ddof=1)
#土鸡的出售价格
y = [7.00,14.1,19.00,22.00,35.00,40.00,42.00]
X_new = np.stack((X,y),axis=0)
print(X_new)
#计算协方差矩阵 [cov(x,x) cov(x,y) cov(y,x) cov(y,y]
cov=np.cov(X_new)
print("协方差矩阵 cov=",cov)
#取协方差xy对角线上的元素
cov_xy=cov[0,1]
#计算贝塔b模型系数: beta = cov_xy/var_X
print("贝塔 ",beta)
-----------------
可以看到beta值为 11.8521706587

3、求解模型系数alpha(a)
a = avg(y) - b * avg(x)
其中avg(y)代表训练数据y的均值, avg(x)代表训练数据x的均值
b是上一步骤求解的beta值
#计算x,y的均值
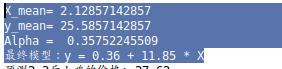
print("X_mean=",np.mean(X))
print("y_mean=",np.mean(y))
#计算alpha, y_mean = alpah + beta* x_mean
alpha = np.mean(y) -beta* np.mean(X)
print("Alpha = ",alpha)
print("最终模型:y = %.2f + %.2f * X" %(alpha,beta))
---------------
Alpha = 0.35752245509
最终模型:y = 0.36 + 11.85 * X
4、到了这一步骤,我们已经求解出完整的模型:y = 0.36 + 11.85 * X
5、根据模型预测一个新的X对应的期望值,如x =2.3,通过如下代码可以预测2.3斤土ji的价格: 27.62
#使用模型预测新的Xy_20 = alpha + beta* 2.3
print("预测2.3斤土ji的价格: %.2f" %y_20)

1、sk-learn机器学习算法库直接提供了线性回归的模型我们可以直接使用,使用方法如下:
1)构建LinearRegression模型
2)使用模型进行拟合训练数据
3)使用拟合后的模型进行预测
#一元线性回归模型 y = a +bX
model = LinearRegression()
model.fit(X,y)
newX = 2.3
newY = model.predict(newX)
print(newY)
print("预测一只 %.1f 斤的土ji价格:%.2f 元" %(newX,newY[0]))
-----------
预测一只 2.3 斤的土ji价格:27.62 元, 和我们之前求解的模型预测值一致。

1、import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression
#自定义字体,解决中文显示问题
plt.rcParams['font.family'] = ['Microsoft YaHei']
plt.rcParams['axes.unicode_minus'] = False
#重量 训练集,拟合时一维数组需要使用[]
X = [[0.5],[1.1],[1.5],[2.2],[3.0],[3.2],[3.4]]
#出售价格
y = [[7.00],[14.10],[19.00],[22.00],[35.00],[40.00],[42.00]]
plt.figure()
plt.title("土ji价格与重量的数据")
plt.xlabel("重量(斤)")
plt.axis(([0,8,0,60]))
plt.grid(True)
#画点
plt.plot(X,y,'r.')
#一元线性回归模型 y = a +bX
model = LinearRegression()
model.fit(X,y)
newX = 2.3
newY = model.predict(newX)
print(newY)
print("预测一只 %.1f 斤的土ji价格:%.2f 元" %(newX,newY[0]))
#预测多个值, 绘制不同的模型直线
X2 = [[0.5],[2.3],[4.2],[6.6]]
y2 = model.predict(X2)
plt.plot(X2,y2,'y-.')
plt.figure()
y3 = [30,30,30,30]
y4 = y2 * 0.4 +4
plt.plot(X2,y3,'r-.')
plt.plot(X2,y4,'b-.')
model.fit(X[1:-1],y[1:-1])
y5 = model.predict(X2)
plt.plot(X2,y5,'g-.')
#cost function
plt.figure()
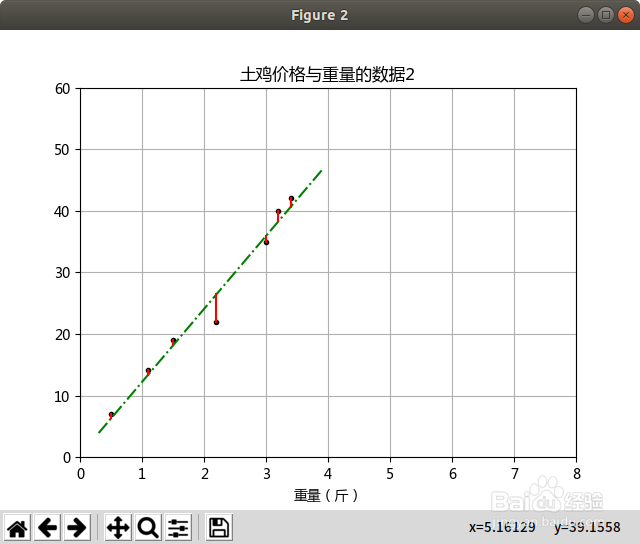
plt.title("土ji价格与重量的数据2")
plt.xlabel("重量(斤)")
plt.axis(([0,8,0,60]))
plt.grid(True)
plt.plot(X,y,'k.')
model2 =LinearRegression()
model2.fit(X,y)
#根据默认拟合的模型进行X2的预测
X2 = [[0.3],[1.2],[2.7],[3.9]]
y2 = model2.predict(X2)
plt.plot(X2,y2,'g-.')
#使用模型预测已有X的预测值
y0 = model2.predict(X)
print(enumerate(X))
#绘制预测值与真实值的差值
for idx,x in enumerate(X):
print("idx= %s" %idx)
plt.plot([x,x],[y[idx],y0[idx]],'r-')
#计算差值平方和,实现模型最佳拟合:有公式
fangchapingfang = np.mean((model2.predict(X)- y)**2)
print("模型的残差值平方和:%.2f " %fangchapingfang)
################# 根据训练数据求解y=a+b*x模型的参数a和b 效果和直接使用sklearn.linear_model一致##########################
#计算方差:有公式, ddof贝塞尔校正系数
#方差是用来衡量样本分散程度的
var_X = np.var(X,ddof=1)
print("方差 %f" %var_X)
#计算协方差
#将X,y组合成一个矩阵
X = [0.5,1.1,1.5,2.2,3.0,3.2,3.4]
var_X = np.var(X,ddof=1)
#出售价格
y = [7.00,14.1,19.00,22.00,35.00,40.00,42.00]
X_new = np.stack((X,y),axis=0)
print(X_new)
#计算协方差矩阵 [cov(x,x) cov(x,y) cov(y,x) cov(y,y]
cov=np.cov(X_new)
print("协方差矩阵 cov=",cov)
#取协方差xy对角线上的元素
cov_xy=cov[0,1]
print("xy协方差值:" ,cov_xy)
#计算贝塔
beta = cov_xy/var_X
print("贝塔 ",beta)
#计算x,y的均值
print("X_mean=",np.mean(X))
print("y_mean=",np.mean(y))
#计算alpha, y_mean = alpah + beta* x_mean
alpha = np.mean(y) -beta* np.mean(X)
print("Alpha = ",alpha)
print("最终模型:y = %.2f + %.2f * X" %(alpha,beta))
#使用模型预测新的X
y_20 = alpha + beta* 2.3
print("预测2.3斤土ji的价格: %.2f" %y_20)
plt.show()