如何证明函数在定义域上有界的充分必要条件是它在定义域上既有上界又有下界

设函数f(x)在定义域A上有界，则存在正实数k，对任意x∈A，|f(x)|<k成立。即-k<f(x)<k成立。所以f(x)在A上有上界k，下界-k。

反过来，f(x)在定义域A上既有上界M又有下界m，即存在实数m，M，对任意对任意x∈A，m<f(x)|<M成立。取k=max{|m|，|M|}，则有对任意对任意x∈A，|f(x)|<k成立。所以f(x)在A上有界。

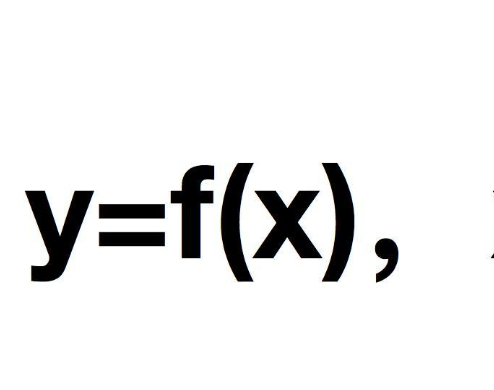
定义域指自变量x的取值范围。

定义域是函数三要素（定义域、值域、对应法则）之一，对应法则的作用对象。求函数定义域的题型主要包括抽象函数，一般函数，函数应用题三种。