如何解二元一次不等式

1、1.Ax+By+C>0或Ax+By+C<0（A、B均不为零）

2.Ax+By+C=0是一直线方程，它有无数组实数解。且所有解（x，y）都是方程的解。

2、二元一次不等式c或Ax+By+C<0的解，表示平面内直线Ax+By+C=0将平面划分的两个不同的区域。

1、根据不等式的基本性质，只需讨论Ax+By+C>0即可。

因为B≠0，所以Ax+By+C>0可变形为y>Kx+b(B>0)或者y<Kx+b(B<0)

2、于是可以看出，y>Kx+b表示直线y=Kx+b上方区域。

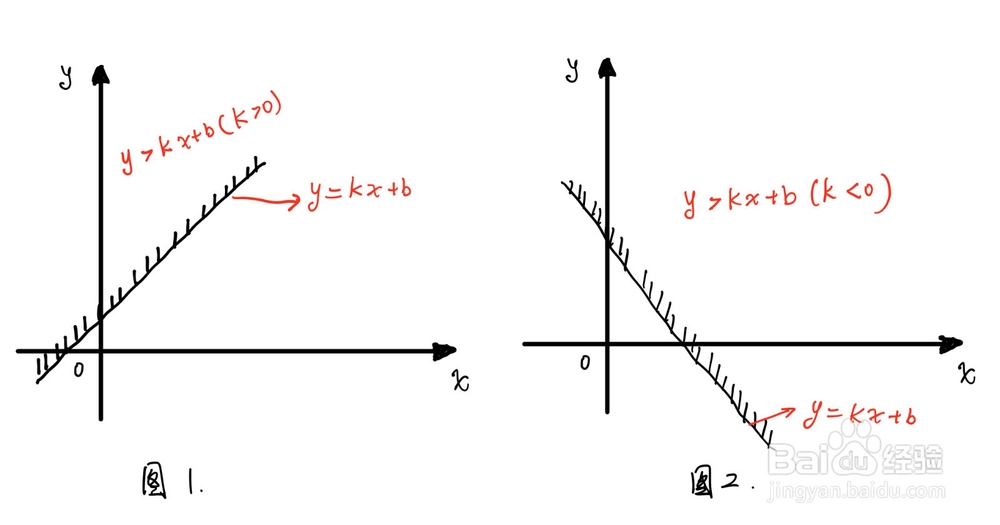
若 K>0, y>Kx+b表示直线y=Kx+b左上方区域，如图1

若 K<0, y>Kx+b表示直线y=Kx+b右上方区域，如图2

3、y<Kx+b表示直线y=Kx+b下方区域。

若 K>0, y<Kx+b表示直线y=Kx+b右下方区域，如图3

若 K<0, y<Kx+b表示直线y=Kx+b左下方区域，如图4

4、对于直线Ax+By+C=0，若A、B中有一个为零，则有x=M或y=N

5、x>M表示直线x=M右侧区域，如图5，而x<M表示直线x=M左侧区域，如图6.

6、y>N表示直线y=N上方区域，如图7，而y<N表示y=N下方区域，如图8.

1、如求2x-y+1<0，即y>2x+1，它表示y=2x+1的左上方区域。如图9

1、二元一次不等式的解是一个坐标平面被一条直线分割成的两个区域的其中一个，其解为一系列的坐标点，结合坐标图像来表示。