弦切角定理证明
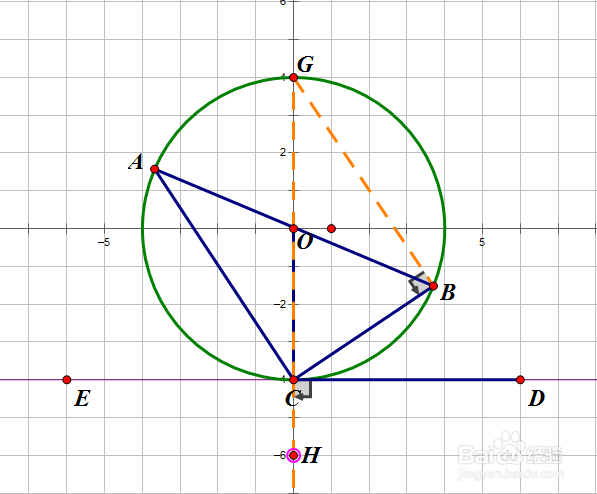
1、定理内容:顶点C在圆上一边BC与圆相交,一边CD与圆相切的角叫弦切角(∠BCD)。则弦切角BCD与其夹着的弧BC所对的圆周角CAB相等。
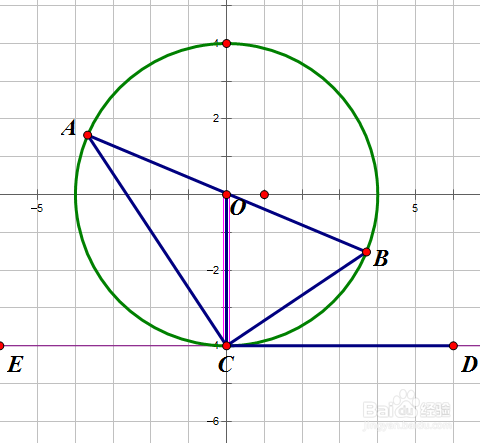
2、辅助线:做一条圆O的过点C的直径交圆于C、G,连BG
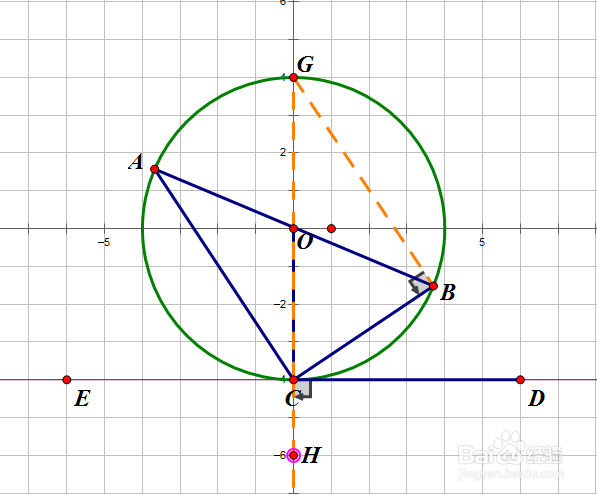
3、由于等弧对等角,所以∠BAC=∠CGB
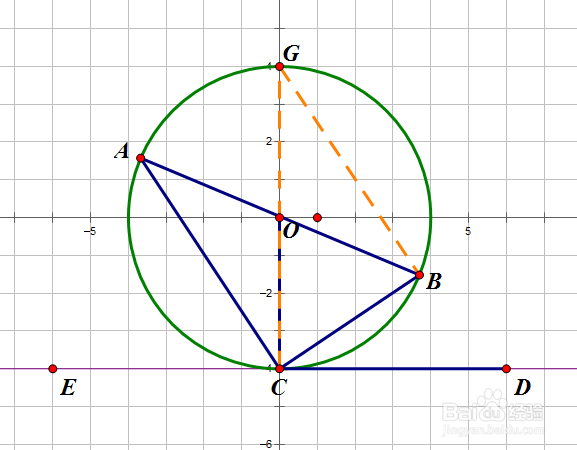
4、由于∠GBC所对的弦为直径,所以∠GBC=∠HCD=90°
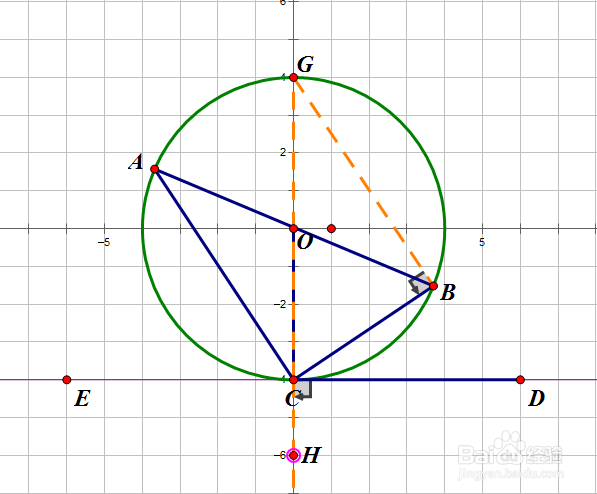
5、在△CBG中,∠CBG+∠CGB=∠BCH=∠BCD+∠HCD(外角定理)
所以∠CGB=∠BCD
所以∠BCD=∠CAB
得证
声明:本网站引用、摘录或转载内容仅供网站访问者交流或参考,不代表本站立场,如存在版权或非法内容,请联系站长删除,联系邮箱:site.kefu@qq.com。
阅读量:92
阅读量:153
阅读量:71
阅读量:113
阅读量:166