用Mathematica让3D图形动起来
1、 画一个单位正方体,再让它绕z轴旋转,代码如下:
Animate[Graphics3D[Rotate[Cuboid[], n Degree, {0, 0, 1}]], {n, 0, 360,1}]

2、 让各面半透明化,可以更好地观察整个图形:
Animate[Graphics3D[{Opacity[.5],
Rotate[Cuboid[], n Degree, {0, 0, 1}]}, Boxed -> False], {n, 0, 360, 1}]

3、 再画一个稍微复杂的图形:
Animate[Graphics3D[{PointSize[0.03], Opacity[.5],
Rotate[{EdgeForm[Blue],
PolyhedronData["TruncatedDodecahedron", "Faces"],
Style[Point[
PolyhedronData["TruncatedDodecahedron", "VertexCoordinates"]],
Opacity[1], Red]}, n Degree, {0, 0, 1}, {0.5, 0.5, 0}]},
Boxed -> False], {n, 0, 360, 1}]

4、 Mathematica还能旋转文本:
Animate[Rotate[Style[Sqrt[b^2 - 4 a c], Bold, Red, 30], n Degree], {n, 0, 360, 1}]

1、 可以把文字旋转60°:
Rotate[把图形旋转60°, 60 Degree]
运行以后:

2、 再旋转一次文字:
Rotate[Style[把图形旋转60°, Bold, Green, 90], 60 Degree]

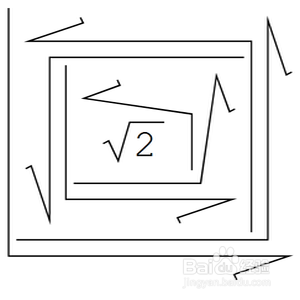
3、 可以反复地旋转数学式子里的根号:
Nest[Rotate[Sqrt[#], 90 °] &, 2, 8]
运行结果是文本形式,下面是截图:
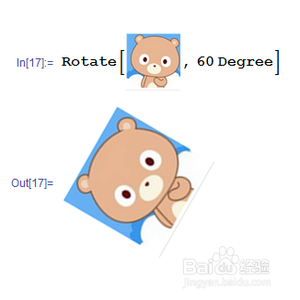
4、 图片也可以旋转:
Rotate[pic, 60 Degree]
只要把你的图片取代pic就可以旋转了!
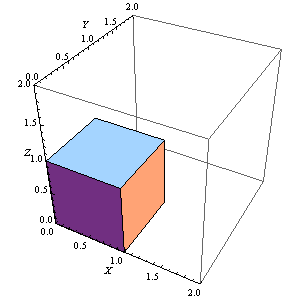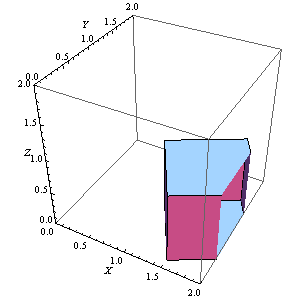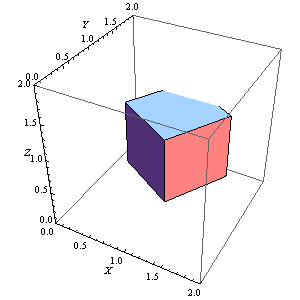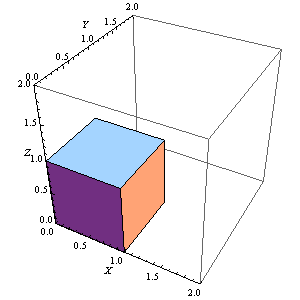
5、 固定正方体的一条棱,让正方体绕着这条棱旋转:
Manipulate[
Graphics3D[Rotate[Cuboid[], n Degree, {0, 0, 1}, {1, 1, 1}],
Axes -> True, AxesLabel -> {X, Y, Z},
PlotRange -> {{0, 2}, {0, 2}, {0, 2}}], {n, 0, 360, 1}]
有一段时间,正方体消失了一部分,这需要调整PlotRange。
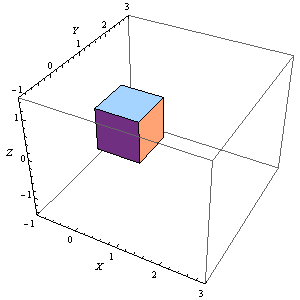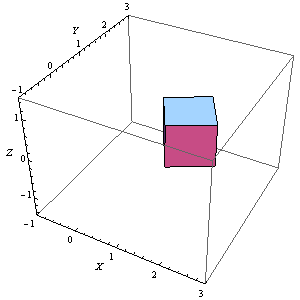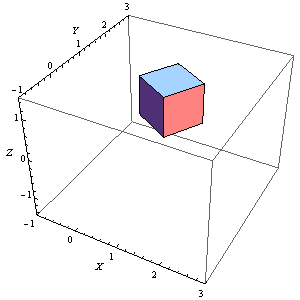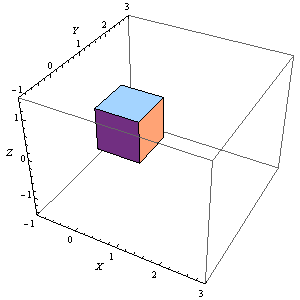
6、Manipulate[
Graphics3D[Rotate[Cuboid[], n Degree, {0, 0, 1}, {1, 1, 1}],
Axes -> True, AxesLabel -> {X, Y, Z},
PlotRange -> {{-1, 3}, {-1, 3}, {-1.5, 1.5}}], {n, 0, 360, 1}]
这个正方体是完整的。
7、 请思考一下下面这个圆柱体旋转轴是在哪里:
Manipulate[
Graphics3D[{Opacity[0.7],
Rotate[Cylinder[], n Degree, {{1, 1, 0}, {0, 0, 1}}]}, Boxed -> False],
{n, 0, 360, 1}]

8、 一个多边形的多次旋转的痕迹:
Graphics[Outer[
Rotate[Rotate[Line[{{1, 0}, {Sqrt[3], 1}/2}], #, {0, 0}], #2, {1,
0}] &, Pi/6 Range[12], Pi/6 Range[12]]]
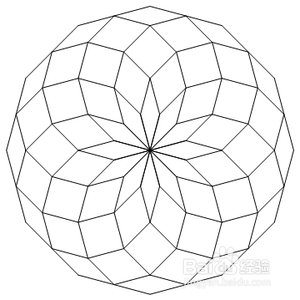
1、 绘制旋转的彩色球体。
先自定义四个函数:
p1[\[Theta]_] := RotationTransform[\[Theta], {0, 0, 1}][{0, 2, 0}];
p2[\[Theta]_] :=
RotationTransform[\[Theta] + Pi/2, {1, 0, 1}][{0, 2, 0}];
p3[\[Theta]_] :=
RotationTransform[\[Theta] + Pi, {1, 0, 0}][{0, 2, 0}];
p4[\[Theta]_] :=
RotationTransform[\[Theta] + 3 Pi/2, {1, 0, -1}][{0, 2, 0}];
然后运行下面的代码:
Animate[Graphics3D[Sphere[],
Lighting -> {{"Point", Red, p1[\[Theta]]}, {"Point", Green,
p2[\[Theta]]}, {"Point", Blue, p3[\[Theta]]}, {"Point", Yellow,
p4[\[Theta]]}}], {\[Theta], 0, 2 Pi},
AnimationDirection -> ForwardBackward, SaveDefinitions -> True,
AnimationRunning -> False]

2、 绘制一个旋转的阴阳双鱼太极图:
f[x_] := Graphics[
Rotate[{Disk[{0, 0}, 1, {Pi/2, (3 Pi)/2}],
Disk[{0, 1/2}, 1/2], {White, Disk[{0, -(1/2)}, 1/2]}, {White,
Disk[{0, 1/2}, 0.1]}, {Disk[{0, -(1/2)}, 0.1]}, Circle[]},
x Degree], Axes -> False, PlotRange -> 1]
Animate[f[a], {a, 0, -359,1}]

3、 用ViewPoint使得一个半透明的贝壳旋转:
Manipulate[
ParametricPlot3D[{1.16^v Cos[v] (1 + Cos[u]), -1.16^v Sin[
v] (1 + Cos[u]), -2 1.16^v (1 + Sin[u])}, {u, 0, 2 Pi}, {v, -15,
6}, Mesh -> None, PlotStyle -> Opacity[0.6], PlotRange -> All,
PlotPoints -> 25, Boxed -> False, Axes -> False,
ImageSize -> {500, 500}, ViewPoint -> {Cos@a, Sin@a, 0.5}], {a, 0,
360 Degree, 10 Degree}]
