Minkowski度量的演示（Mathematica）

1、Minkowski度量的定义：

给定平面上的两个点A和B，它们的距离用下图公式表示。

当n=2，就是最常见的欧几里德度量。

2、当n=3的时候，单位圆是什么样子呢？

n = 3;

ContourPlot[

 Power[Abs[x - 0]^n + Abs[y - 0]^n, (n)^-1] == 1, {x, -2, 2}, {y, -2, 

  2}]

3、当n=1的时候，单位圆的样子。

4、n=0.5时的单位圆。

5、等高线图：

n = 0.5;

ContourPlot[Power[

 Abs[x - 0]^n + Abs[y - 0]^n, (n)^-1], {x, -2, 2}, {y, -2, 2}, 

 Contours -> 20]

6、n=36时的单位圆。

7、以{0,±1}为焦点的椭圆：

n = 3;

ContourPlot[

 Power[Abs[x]^n + Abs[y - 1]^n, (n)^-1] + Power[

   Abs[x]^n + Abs[y + 1]^n, (n)^-1] == 2.01, {x, -2, 2}, {y, -2, 2},

 PlotPoints -> 50]

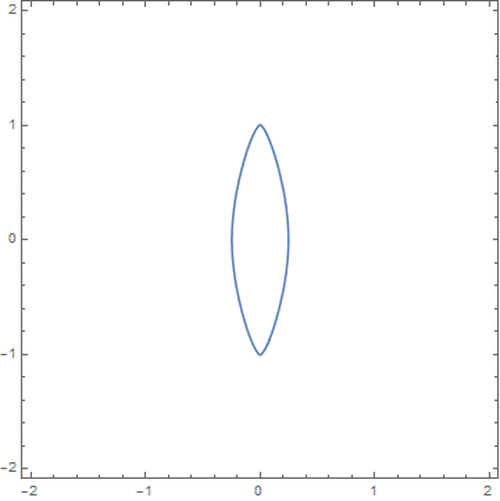
8、n=3，当Power[Abs[x]^n + Abs[y - 1]^n, (n)^-1] + Power[

  Abs[x]^n + Abs[y + 1]^n, (n)^-1] == 2

图像是一条线段。

9、n=0.5时候的椭圆：

n = 0.5;

ContourPlot[

 Power[Abs[x]^n + Abs[y - 1]^n, (n)^-1] + Power[

   Abs[x]^n + Abs[y + 1]^n, (n)^-1] == 3, {x, -2, 2}, {y, -2, 2}]

10、上面的等高线图。

n = 0.5;

ContourPlot[

 Power[Abs[x]^n + Abs[y - 1]^n, (n)^-1] + Power[

  Abs[x]^n + Abs[y + 1]^n, (n)^-1], {x, -2, 2}, {y, -2, 2}, 

 Contours -> 20]

11、n=1对应的椭圆的等高线图。

12、n=8对应的等高线图。