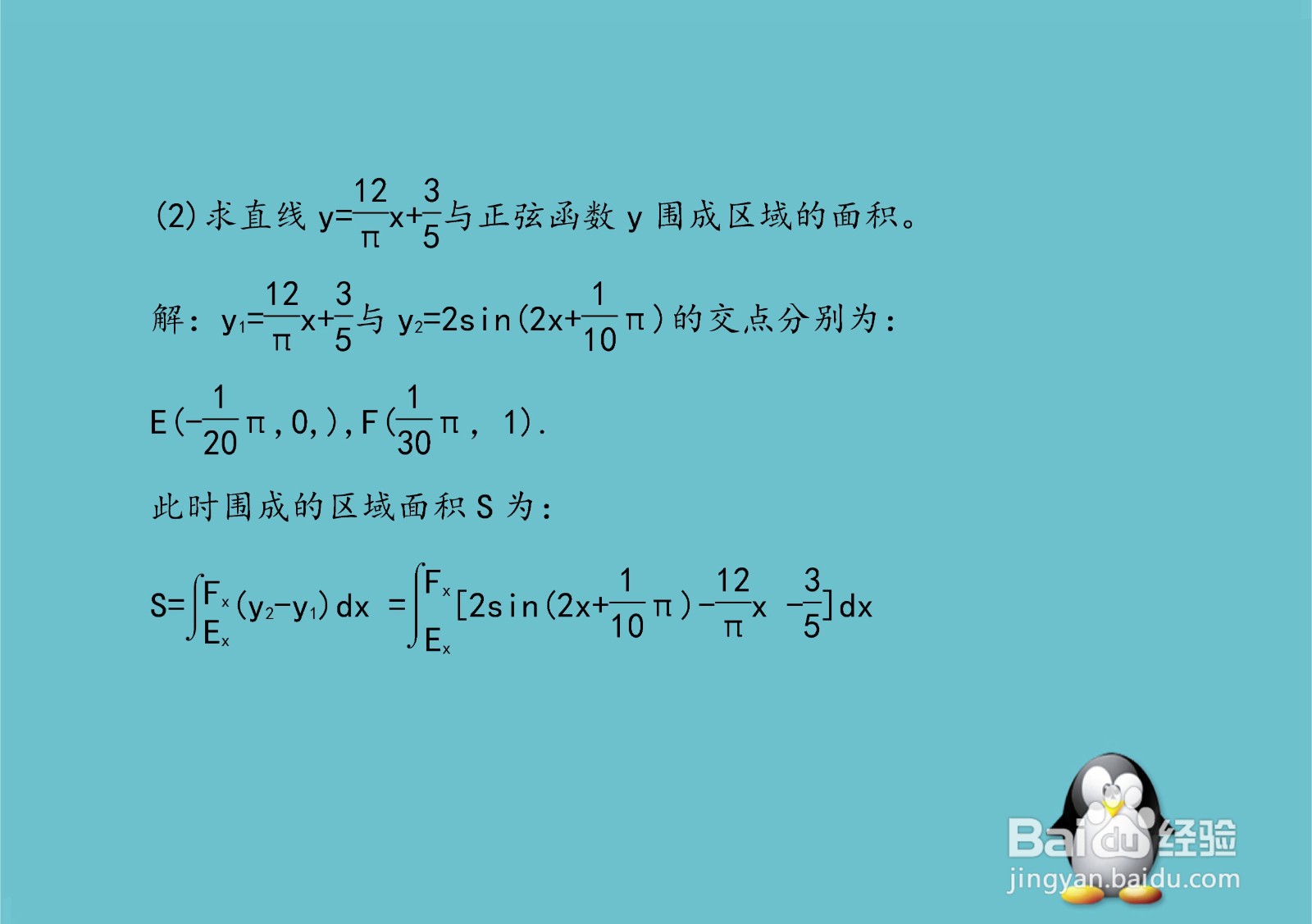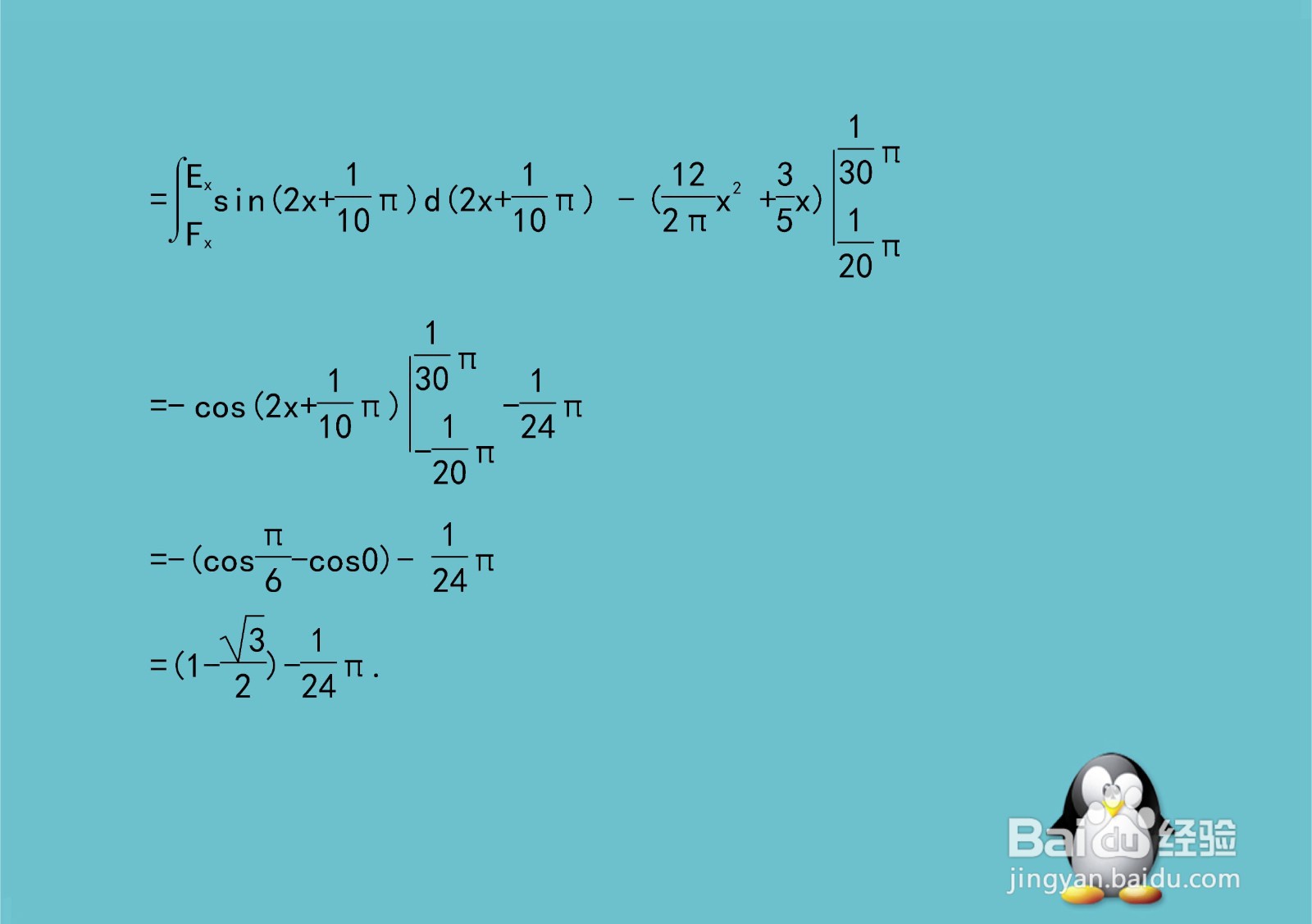正弦函数y=2sin(2x+π/10)的周期单调等性质

1、三角函数y=2sin(2x+π/10)的定义域、值域、单调、周期、对称轴、切线等有关性质。

1、当2x+π/10=0时，有：

x=-1/20*π.

即该函数y的中心对称点为：（-1/20*π，0）。

2、单调增区间

2kπ-π/2≤2x+π/10≤2kπ+π/2,k∈Z，

2kπ-π/2-π/10≤2x≤2kπ+π/2-π/10,

2kπ-3π/5≤2x≤2kπ+2π/5

kπ-3π/20≤x≤kπ+π/5

即该函数的单调增区间为:

[kπ-3π/20,kπ+π/5]

3、单调减区间

2kπ+π/2≤2x+π/10≤2kπ+3π/2,k∈Z，

2kπ+π/2-π/10≤2x≤2kπ+3π/2+π/10,

2kπ+ 2π/5≤2x≤2kπ+8π/5

kπ+ 1π/5≤x≤kπ+4π/5

即该函数的单调增区间为:

[kπ+π/5,kπ+4π/5]

1、求函数的导数及高阶导数的步骤为。

2、y=2sin(2x+π/10)，则：

y '=4cos(2x+π/10).

(1)在点A((1/30)π，1)处，有：

y '=4cos[2*(1/30)π+π/10]=4cosπ/6=4√3/2,

则该点处的切线方程为：

y-1=4√3/2[x-(1/30)π]。

3、在点B（(23/40)π，-2√2/2）处，有：

y '=4cos[2*(23/40)π+π/10]=4cos5π/4=-4√2/2,

则该点处的切线方程为：

y+√2=-4√2/2[x-(23/40)π]。

4、求图像半个周期内与x轴围成的面积。

解：先求其中半个周期内x的坐标点，即：

C(-(1/20)π,0,),D((1/5)π,0).

此时围成的区域面积为：

S=∫[Cx，Dx]ydx

=∫[Cx，Dx]2sin(2x+π/10)dx

=∫[Cx，Dx]sin(2x+π/10)d(2x+π/10)

=-cos(2x+π/10)[-(1/20)π,(1/5)π]

=-(cosπ/2-cos0)

=1.

5、求直线y=12x/π+(3/5)与正弦函数y围成区域的面积。

解：y1=12x/π+(3/5)与y2=2sin(2x+π/10)

的交点分别为：

E(-(1/5)π,0,),F((1/30)π，1).

此时围成的区域面积S为：

S=∫[Ex，Fx](y2-y1)dx

=∫[Ex，Fx][2sin(2x+π/10)-12x/π-(3/5)]dx

=∫[Ex，Fx]sin(2x+π/10)d(2x+π/10)

-[12x^2/2π+(3/5)x][Ex，Fx]

=-cos(2x+π/10)[Ex，Fx]-1/24π

=-(cosπ/6-cos0)-1/24π

=2(2-√3)/4-1/24π.