费马点的证明与背景分别是什么

费马点的证明：

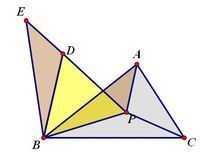
如图，在△ABC中，P为其中任意一点。连接AP，BP，得到△ABP。

以 点B为旋转中心，将 △ABP逆时针旋转 60°，得到△EBD

∵旋转60°，且BD=BP，

∴△DBP 为一个等边三角形

∴PB=PD

因此， PA+PB+PC=DE+PD+PC

由此可知当E、D、P、C 四点共线时， 为PA+PB+PC最小

若E、D、P共线时，

∵等边△DBP

∴∠EDB=120°

同理，若D、P、C共线时，则 ∠CPB=120°

∴P点为满足∠APB=∠BPC=∠APC=120° 的点。

背景：

费马点问题最早是由法国数学家皮埃尔·德·费马在一封写给意大利数学家埃万杰利斯塔·托里拆利（气压计的发明者）的信中提出的。

托里拆利最早解决了这个问题，而19世纪的数学家斯坦纳重新发现了这个问题，并系统地进行了推广，因此这个点也称为托里拆利点或斯坦纳点，相关的问题也被称作费马-托里拆利-斯坦纳问题。这一问题的解决极大推动了联合数学的发展，在近代数学史上具有里程碑式的意义。

费马点的画法：

1.以任意半径画圆0，并作出圆的一条直径AB。

2.以点A(或点B)为圆心，OA(或OB)为半径画出圆A(或圆B)。

3.两圆相交于C点，联结AC，BC。

4.则∠CBA或∠CAB为30°，∠C为90°，两角相加即为120°。

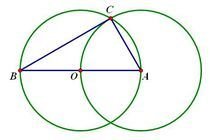
5.若大于等于120°，则该钝角顶点即为该三角形的费马点，若三角形的三个角均小于120°，则继续

做以下步骤。

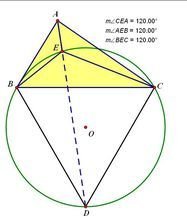
6.以三角形任意一边a向外做等边三角形。

7.找出该等边三角形的外心，并作出外接圆。

8.联结a边所对的两个顶点(连接AD)。

9.该连线与外接圆交点即为该三角形的费马点。