幂指函数的求导方法

1、本例子函数为z=x^y，求z对y的偏导数。

2、在求对y的偏导数时，此时z看做成y的指数函数，x看做成常数。

1、此时变量为x，底数和指数都有变量。

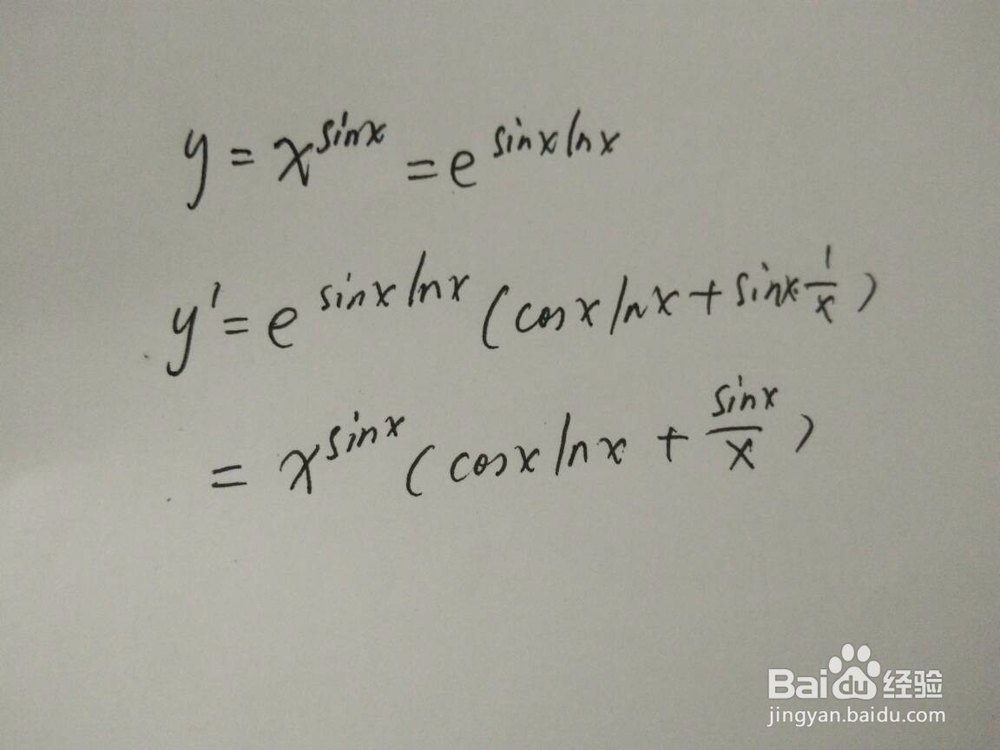
2、求导过程中，需要进行变形，公式为：a^b=e^(blna).

1、此时是幂指函数的方程类型。

2、主要步骤是，通过公式a^b=e^(blna)变形后再对方程两边同时求导。

1、此时是幂指函数的方程类型，求z对x的偏导数。

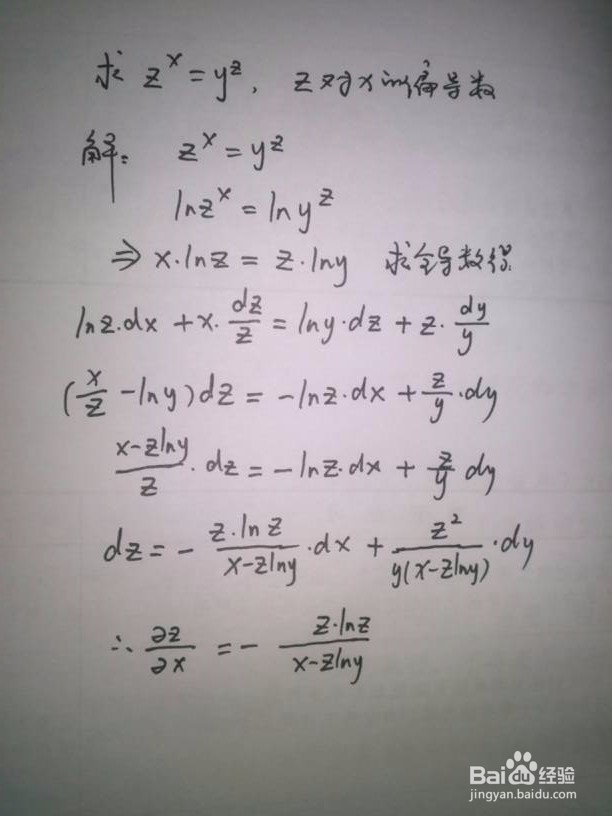
2、主要步骤是，通过公式a^b=e^(blna)变形后再对方程两边同时对x求导，把y看做成常数。

1、此时为幂指函数函数类型，且为隐函数，变量y出现2次。

2、本步骤主要是方程两边取对数后，再对方程两边求导得到。

1、本幂指函数类型为三元函数，需要用到公式a^b=e^(blna)。

2、本例子主要是通过求全导的方式求导数。

1、本幂指函数为幂指函数和的形式，也需要a^b=e^(blna)的公式变换。

2、公式变换后，再对方程两边求导。