双心四边形的作图、性质

1、        给定一个圆，作出它的一个内接四边形，要求这个四边形有内切圆。

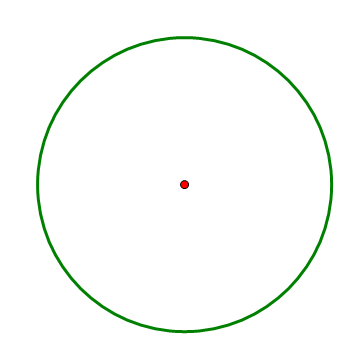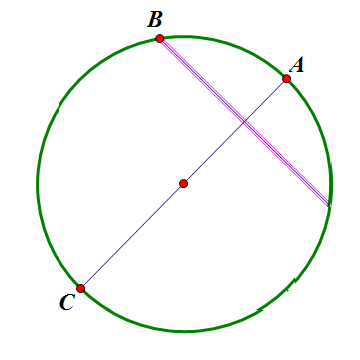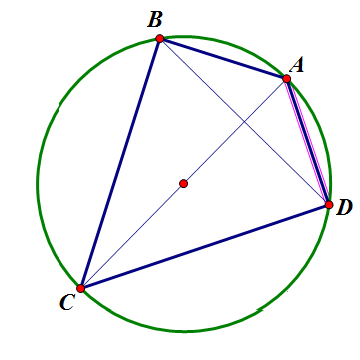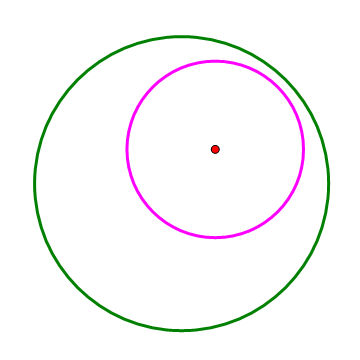
        对于这一点，我说，可以“投机取巧”。我们可以很容易的做出一个内接四边形ABCD，如果AC是直径，B、D关于AC对称，那么ABCD一定有内切圆。我们这么做的理由，就是因为有Poncelet大定理的支持。

        制作动态图不容易！请百度经验管理员用心考虑，是否内容过于简单而导致无法通过您们的审核。

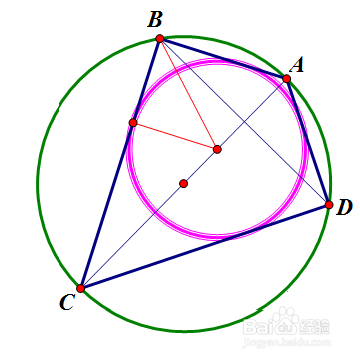
2、        验证一下Poncelet大定理。

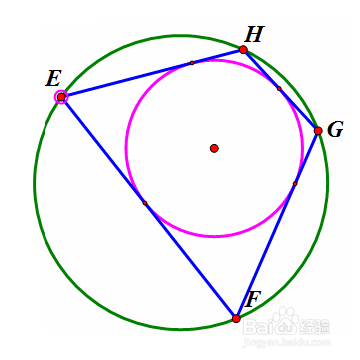
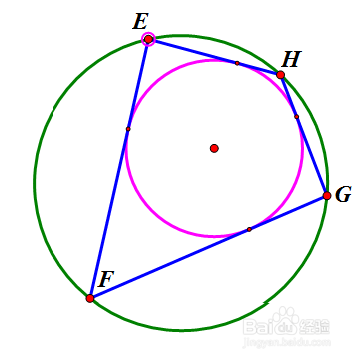
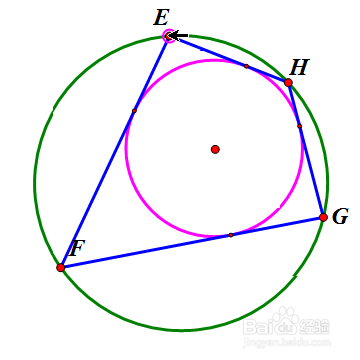
        在大圆上任取一点E，作大圆的弦EF与小圆相切，过F作大圆的另一条弦FG与小圆相切，过G作大圆的另一条弦GH与小圆相切。那么，HE也是小圆的一条切线。看下面的动态图。

        制作动态图不容易，请百度经验管理员用心阅读，是否内容过于简单，而导致无法通过您们的审核。

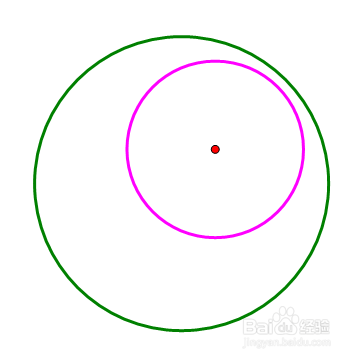
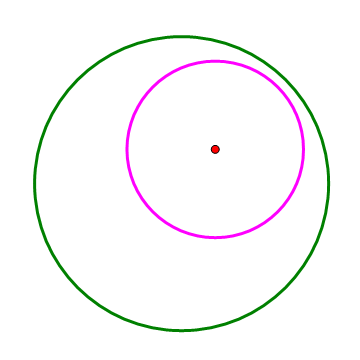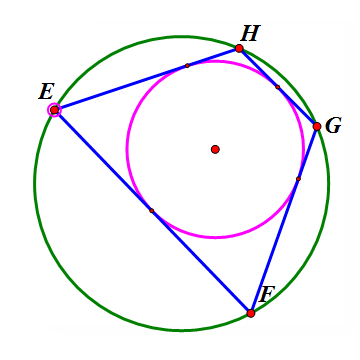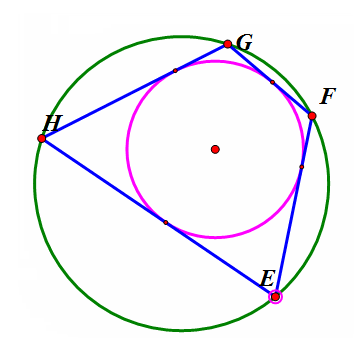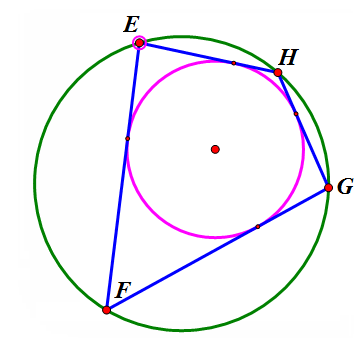
3、        这样，无论点E在圆的什么位置，四边形EFGH都是双心四边形。当H跑到E的位置时，新的四边形HEFG就全等于旧的四边形EFGH。

        制作动态图不容易，请百度经验管理员用心阅读，是否内容过于简单！

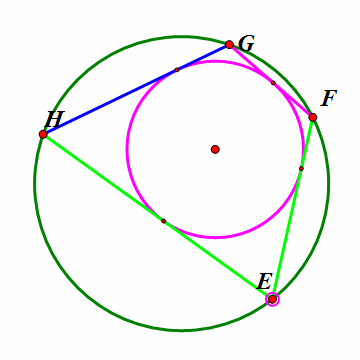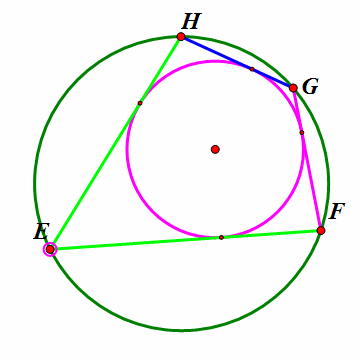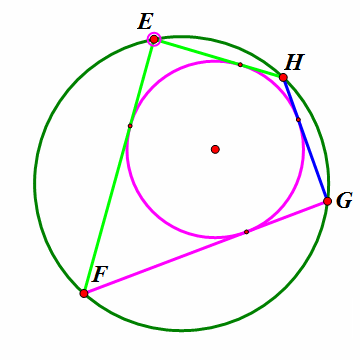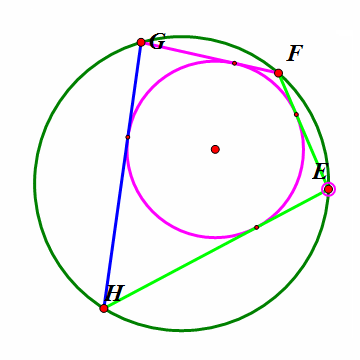
1、        给定一个圆，作出它的一个四个顶点共圆的外切四边形。

        首先，需要知道下面的结论：

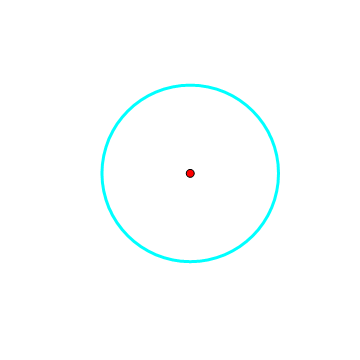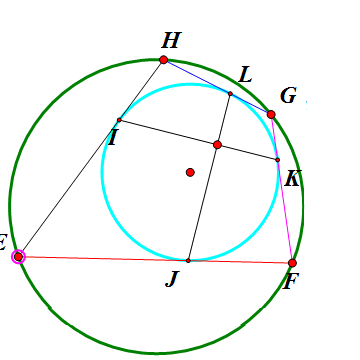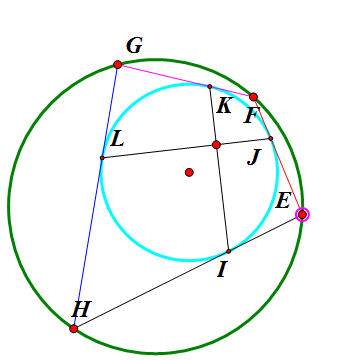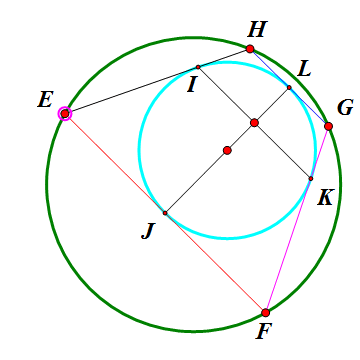
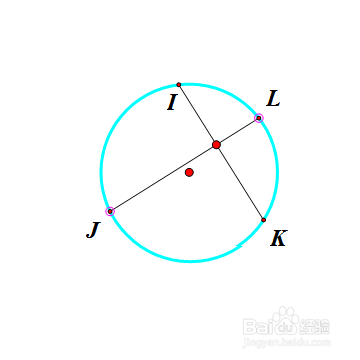
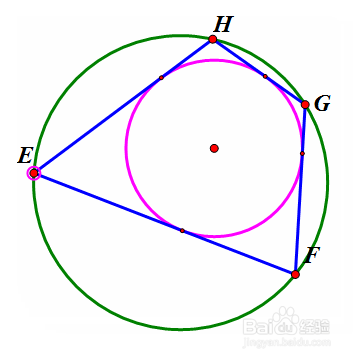
        设EFGH是双心四边形，各边与内切圆的切点分别是J、K、L、I，那么，JL垂直于KI。而且，JL、KI、EG、FH共点（记为N）；当点E在外接圆上移动的时候，N的位置不变。

2、        于是，上面提出的问题就可以轻松解答：

        作圆内任意两条互相垂直的弦，端点分别记为I、J、K、L；

        作此圆的切线，切点分别是I、J、K、L；

        设这四条切线围成四边形EFGH，则E、F、G、H四点共圆。