3阶以内的矩阵求逆矩阵的3种手算方法

1、首先，我们来看如何使用待定系数法，求矩阵的逆。

举例：

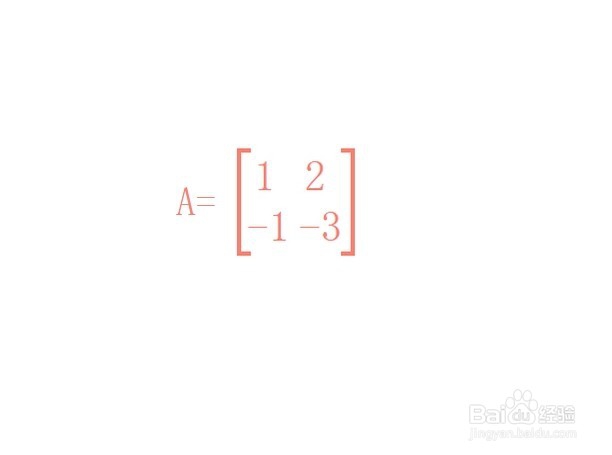
矩阵A=

1 2

-1 -3

2、假设所求的逆矩阵为

a b

c d

则

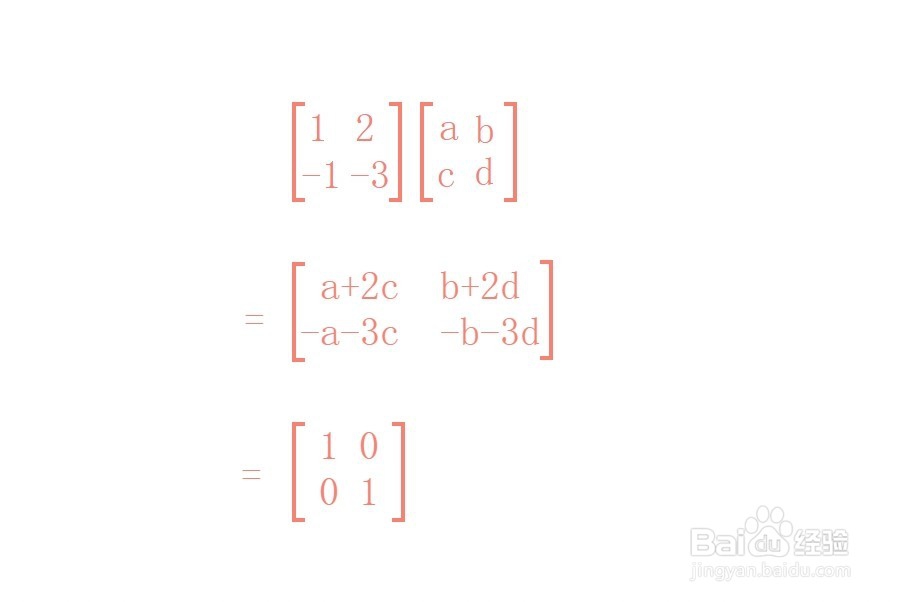
3、从而可以得出方程组

a+2c=1

b+2d=0

-a-3c=0

-b-3d=1

解得

a=3

b=2

c=-1

d=-1

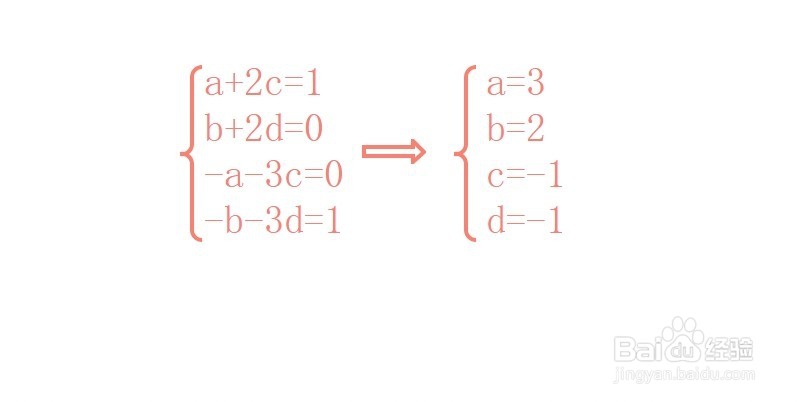
4、所以A的逆矩阵A⁻¹=

3 2

-1 -1

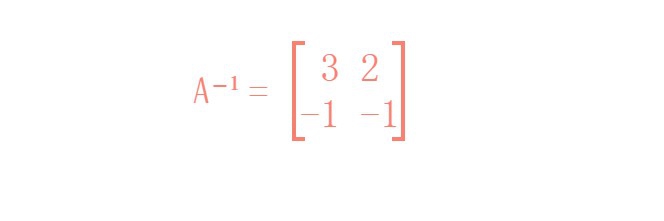
1、伴随矩阵是矩阵元素所对应的代数余子式，所构成的矩阵，转置后得到的新矩阵。

我们先求出伴随矩阵A*=

-3 -2

1 1

2、接下来，求出矩阵A的行列式

|A|

=1*(-3)-(-1)*2 

=-3+2

=-1

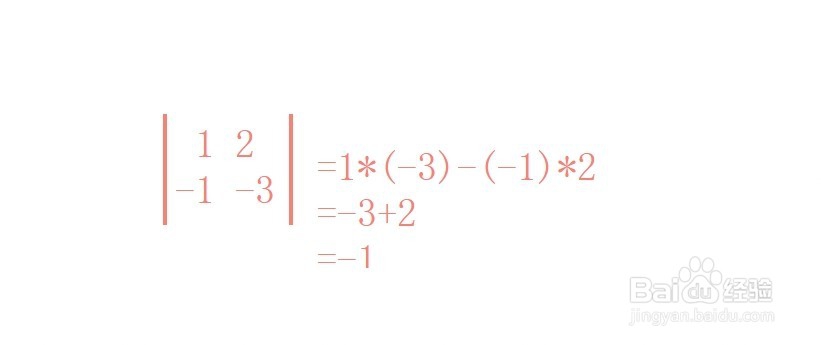
3、从而逆矩阵A⁻¹=A*/|A| = A*/(-1)=-A*=

3 2

-1 -1

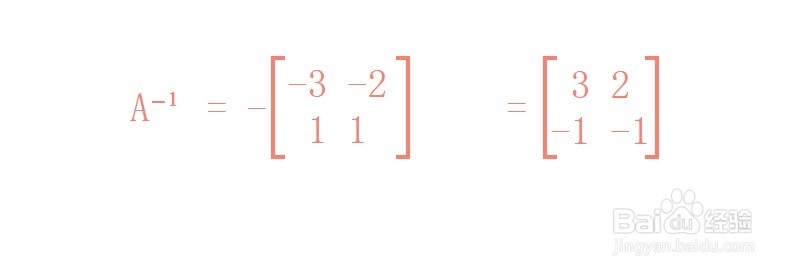
1、下面我们介绍如何通过初等(行)变换来求逆矩阵。

首先，写出增广矩阵A|E，即矩阵A右侧放置一个同阶的单位矩阵，得到一个新矩阵。

 1  2  1  0

-1 -3  0  1

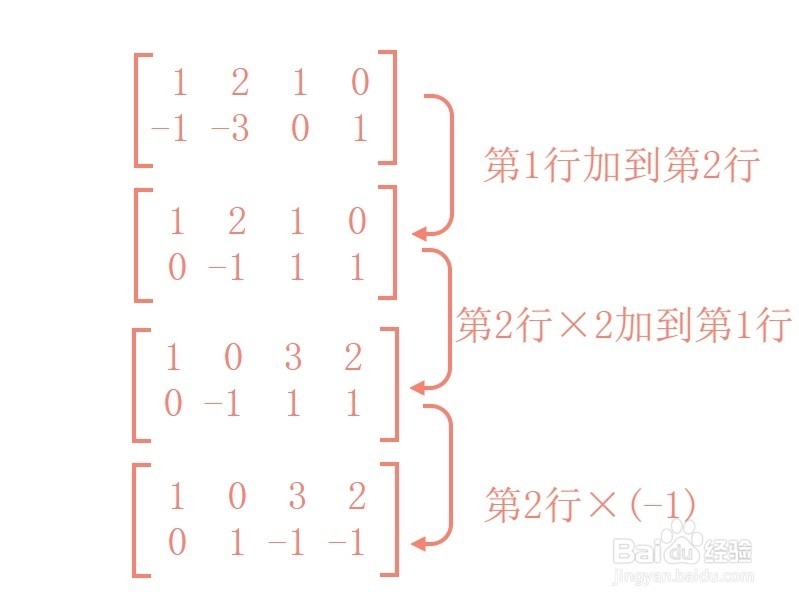
2、然后进行初等行变换。依次进行

第1行加到第2行，得到

 1  2  1  0

 0 -1  1  1

第2行×2加到第1行，得到

 1  0  3  2

 0 -1  1  1

第2行×(-1)，得到

 1  0  3  2

 0  1 -1 -1

3、因此逆矩阵A⁻¹=

3 2

-1 -1