用Mathematica演示“中点迭代”现象

1、给出平面上的100个随机点，顺次连接线段，形成一个折线图形：

pl = RandomPoint[Disk[], 100];

Graphics[{Point[pl],Line[pl]}]

2、依次取各条线段的中点，再顺次连接这些中点，得到新的折线图形：

pl1=Table[(RotateRight[pl,n][[1]]+RotateRight[pl,n][[2]])/2,{n,100}];

{Graphics[{Point[pl],Line[pl],Point[pl1],Line[pl1]}],

     Graphics[{Point[pl1],Line[pl1]}]}

3、再执行一次上面的操作：

pl2=Table[(RotateRight[pl1,n][[1]]+RotateRight[pl1,n][[2]])/2,{n,100}];

{Graphics[{Point[pl1],Line[pl1],Point[pl2],Line[pl2]}],

     Graphics[{Point[pl2],Line[pl2]}]}

4、用Nest对上面的操作进行迭代：

pl100=Nest[Table[(RotateRight[#,n][[1]]+RotateRight[#,n][[2]])/2,

    {n,100}]&,pl,100];

{Graphics[{Point[pl99],Line[pl99],Point[pl100],Line[pl100]}],

     Graphics[{Point[pl100],Line[pl100]}]}

下图就是第100操作之后得到的图形。

5、再看看迭代到1000次的效果图：

pl1000=Nest[Table[(RotateRight[#,n][[1]]+RotateRight[#,n][[2]])/2,

    {n,100}]&,pl,1000];

{Graphics[{Point[pl999],Line[pl999],Point[pl1000],Line[pl1000]}],

     Graphics[{Point[pl1000],Line[pl1000]}]}

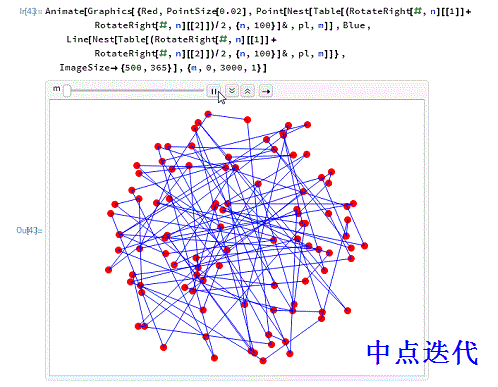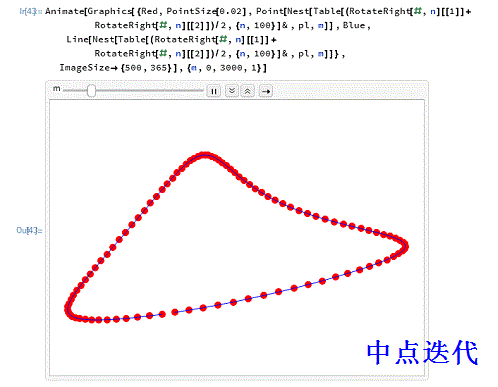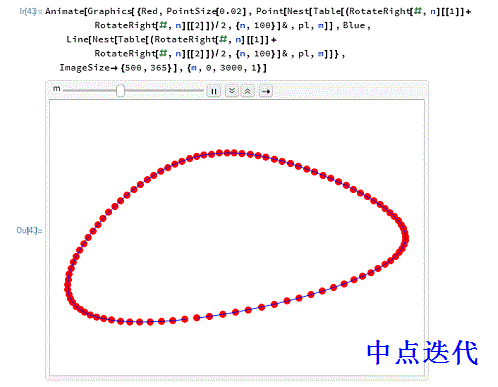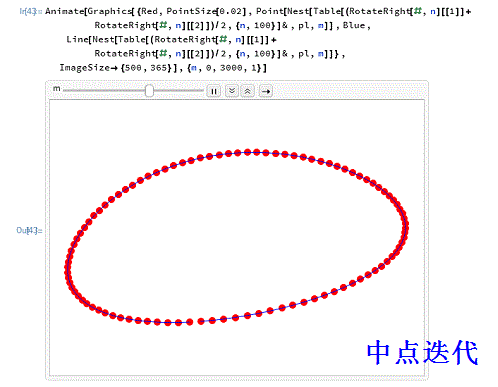
6、用一个动画来演示这个过程的效果，迭代深度定为3000次。