if-else-end结构求判别式和一元二次方程的根
1、第一,求一元二次方程a*x^2+b*x+c=0的根,判别式delta=b^2-4*a*c,delta>0有两个不同的实根,delta=0有两个相同的实根,delta<0没有实根。
启动MATLAB,新建脚本(Ctrl+N),在脚本编辑区输入如下代码:
close all; clear all; clc
a=input('please input ''a'':');
b=input('please input ''b'':');
c=input('please input ''c'':');
delta=b^2-4*a*c;
syms x
if delta>0
fprintf('the equation has two different real roots\n')
X=solve(a*x^2+b*x+c==0);
x1=X(1),x2=X(2)
ezplot(a*x^2+b*x+c);hold on
plot([x1,x2],0,'ro','MarkerSize',10,'MarkerFace','r')
plot([-2*pi:0.1:2*pi],0,'r')
elseif delta==0
fprintf('the equation has two same real roots\n')
X=solve(a*x^2+b*x+c==0);
x=X
else
fprintf('the equation does not have real roots\n')
end
其中solve()是MATLAB自带的求解等式的函数。
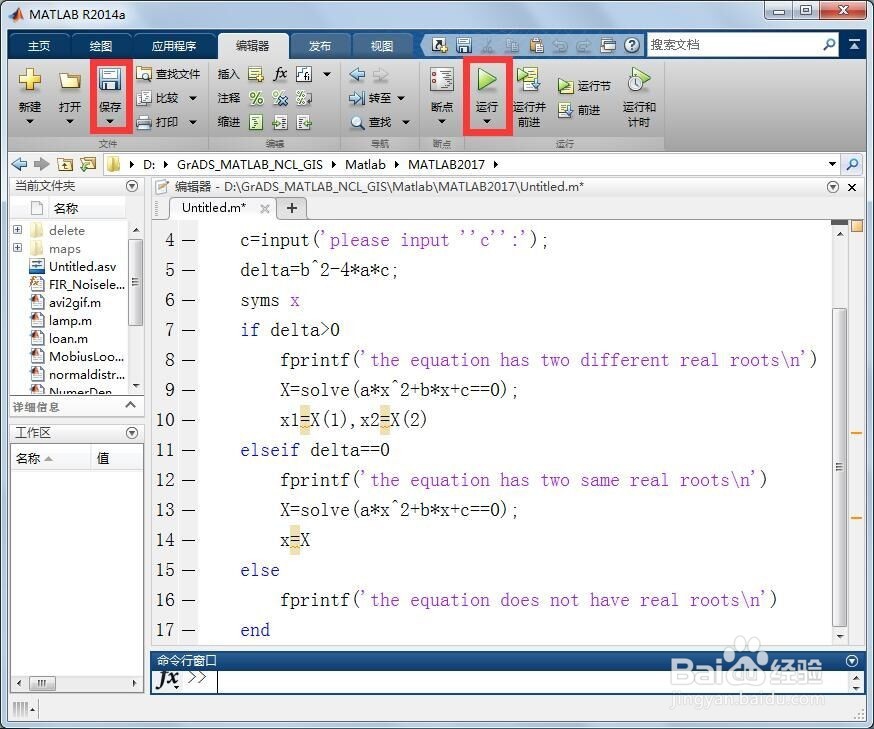
2、第二,保存和运行上述脚本,命令行窗口提示请输入a,b和c。
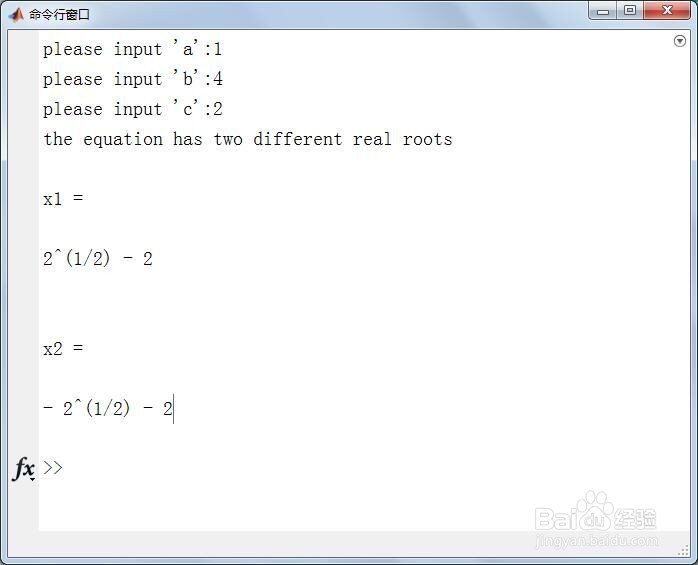
以一元二次方程2*x^2+4*x+1=0为例,运行该脚本并输入a=2,b=4和c=1,则会得到如下结果
please input 'a':1
please input 'b':4
please input 'c':2
the equation has two different real roots
x1 =
2^(1/2) - 2
x2 =
- 2^(1/2) - 2
即一元二次方程2*x^2+4*x+1=0有两个不同的实根。
3、第三,以一元二次方程1*x^2+2*x+1=0为例,运行上述脚本,则得到如下结果。
please input 'a':1
please input 'b':2
please input 'c':1
the equation has two same real roots
x =
-1
-1
即一元二次方程1*x^2+2*x+1=0有两个相等的实根。

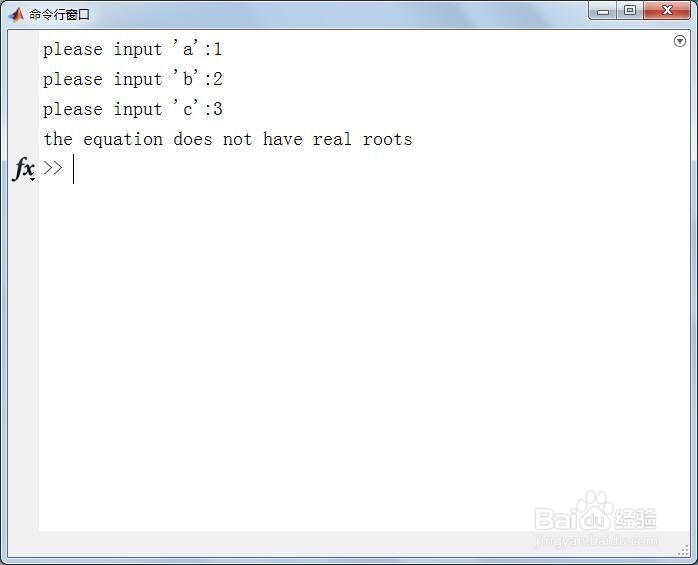
4、第四,以一元二次方程1*x^2+2*x+3=0为例,运行上述脚本,则得到如下结果。
please input 'a':1
please input 'b':2
please input 'c':3
the equation does not have real roots
即一元二次方程1*x^2+2*x+3=0没有实根。
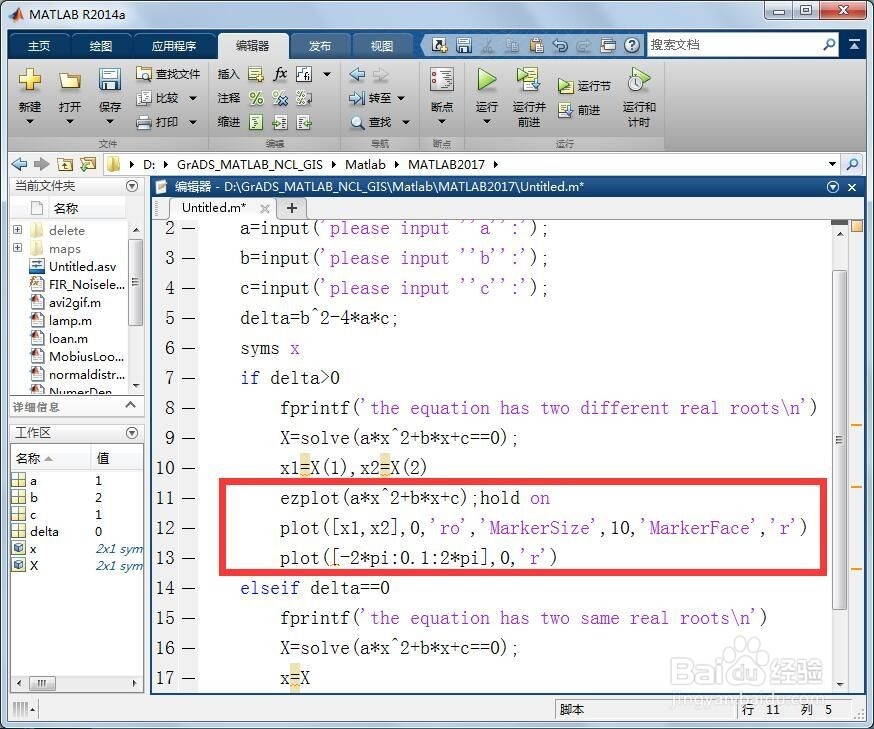
5、第五,在上述脚本的基础上,对于一元二次方程有两个不同实根的情况,要求MATLAB绘制出函数图像和标出两个实数根,只需将脚本改进如下:
close all; clear all; clc
a=input('please input ''a'':');
b=input('please input ''b'':');
c=input('please input ''c'':');
delta=b^2-4*a*c;
syms x
if delta>0
fprintf('the equation has two different real roots\n')
X=solve(a*x^2+b*x+c==0);
x1=X(1),x2=X(2)
ezplot(a*x^2+b*x+c);hold on
plot([x1,x2],0,'ro','MarkerSize',10,'MarkerFace','r')
plot([-2*pi:0.1:2*pi],0,'r')
elseif delta==0
fprintf('the equation has two same real roots\n')
X=solve(a*x^2+b*x+c==0);
x=X
else
fprintf('the equation does not have real roots\n')
end
相比第一步的脚本而言,只是添加三行代码:
ezplot(a*x^2+b*x+c);hold on
plot([x1,x2],0,'ro','MarkerSize',10,'MarkerFace','r')
plot([-2*pi:0.1:2*pi],0,'r')
用于绘制函数图像和标出两个不同的实数根。
6、第六,依旧以一元二次方程2*x^2+4*x+1=0为例,运行上述改进的脚本,不仅可以在命令行窗口得到方程的两个不同的实根,还可以得到如下图像。
