Mathematica基础——计算二重积分

1、计算积分 x^2*y + x，其中积分区域是矩形区域——｛2<=y<=4&&1<=x<=3｝：

Integrate[( x^2*y + x ) Boole[2<=y<=4&&1<=x<=3], {x, -10, 10}, {y, -10, 10}]

2、这其实是求一个曲面柱体的体积。

3、计算积分x^2-y^2，其中积分区域是——｛0<=y<=Sin[x]&&0<=x<=Pi｝：

Integrate[(x^2-y^2) Boole[0<=y<=Sin[x]&&0<=x<=Pi], {x, -10, 10}, {y, -10, 10}]

4、积分区域的形状如下图：

RegionPlot[0<=y<=Sin[x]&&0<=x<=Pi,{x,0,Pi},{y,0,1}

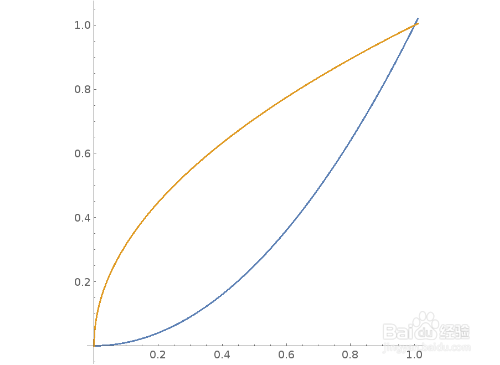
5、计算x*Sqrt[y]的积分，积分区间是曲线y=x^2和曲线y=Sqrt[x]所夹的区域：

Plot[{x^2,Sqrt[x]},{x,0,1.01}]

画出积分区域：

RegionPlot[x^2<=y<=Sqrt[x],{x,0,1.01},{y,0,1.01}]

计算积分：

Integrate[x Sqrt[y] Boole[x^2<=y<=Sqrt[x]],{x, -10, 10}, {y, -10, 10}]