求y=(x+1)^2.(2x^3+2x-1)一阶导数和部分偏导数

1、    本经验的主要内容， 通过取对数法求导法及函数商的求导法则等有关知识，计算函数的导数。

2、       取对数的运算可将幂函数、指数函数及幂指函数运算降格成为乘法运算，可将乘法运算或除法运算降格为加法或减法运算，使求导运算计算量大为减少。

3、     进一步化简，即可得到函数的一阶导数。取对数法：

∵y=(x+1)^2/(2x^3+2x-1)，

∴lny=ln[(x+1)^2/(2x^3+2x-1)],即：

lny=ln(x+1)2-ln(2x3+2x-1)，

lny=2ln(x+1)-ln(2x3+2x-1)，

两边求导得：

y'/y=2/(x+1)-(6x^2+2)/(2x^3+2x-1).

y'=y[2/(x+1)-(6x^2+2)/(2x^3+2x-1)].

为取对数求导数的主要步骤。

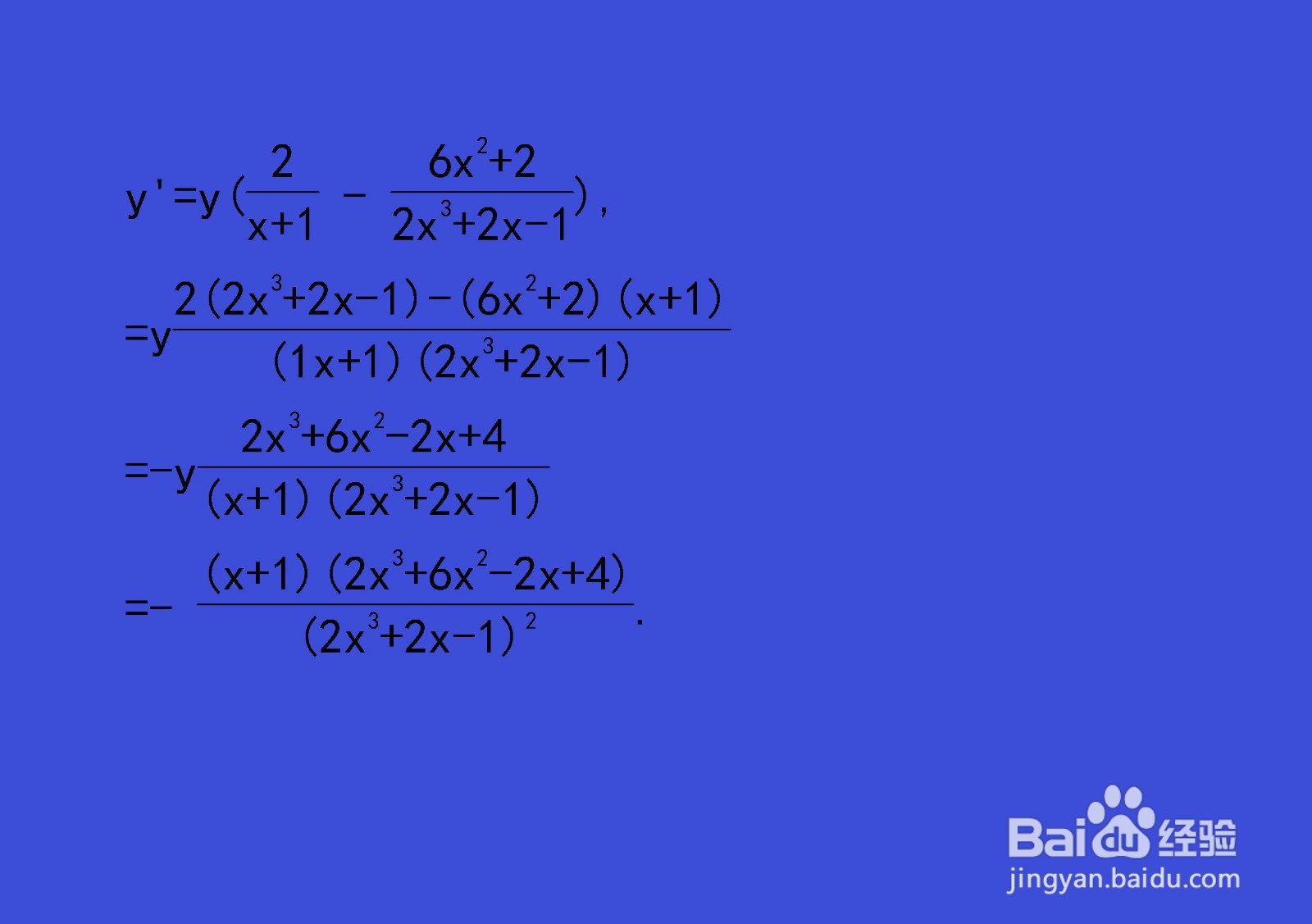
4、利用函数商的求导法则，对函数y求导，也可得函数的一阶导数。

y=(x+1)^2/(2x^3+2x-1)，，使用函数商的求导法则，得：

y'=[2（x+1）（2x^3+2x-1）-(x+1)^2（6x^2+2）]/(2x^3+2x-1)^2,

y'=-(x+1)(2x^3+6x^2-2x+4)/(2x^3+2x-1)^2.

5、使用函数乘积的求导规则，计算该函数y的二阶偏导数过程如下：

因为y'=-(x+1)(2x^3+2x-1)^2./(2x^3+2x-1)^2.

所以：

-y'(2x^3+2x-1)^2=(x+1)(2x^3+2x-1)^2.

6、       二阶导数，是原函数导数的导数，将原函数进行二次求导。一般的，函数y=f(x)的导数y'=f'(x)仍然是x的函数，则y'=f'(x)的导数叫作函数y=f(x)的二阶导数。

7、      再次根据函数商的求导规则，（U/V)'=(U'V-UV')/V^2,根据法则来求函数的二阶偏导数。

8、分子分母分别进行化简，可得函数的二阶导数。

几何的直观解释:如果一个函数f(x)在某个区间I上有f''(x)(即二阶导数)>0恒成立，那么在区间I上f(x)的图象上的任意两点连出的一条线段，这两点之间的函数图象都在该线段的下方，反之在该线段的上方。