Mathematica基础——微分方程可视化(2)

1、求方程的一个特例对应的图形：

2*D[u[x, y], x] + 3*D[u[x, y], y] + u[x, y] == 0

2、微分方程y'[x] + x*y[x] == Cos[x^2]的特解图形。

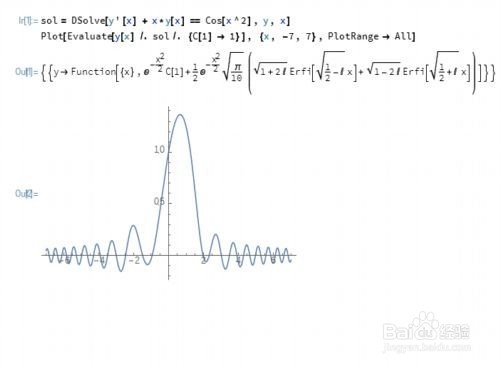
3、线性二阶常微分方程的初值问题：

{y''[x]/y[x] == -4* Exp[-x/4], y[0] == 1, y'[0] == 1/2}

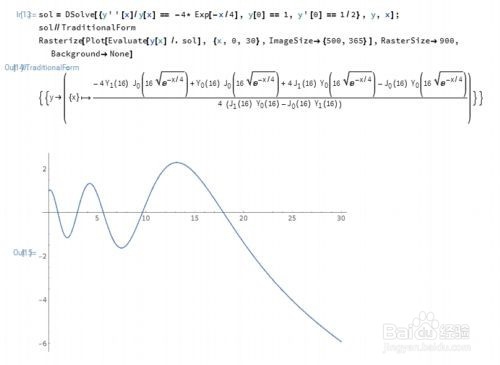
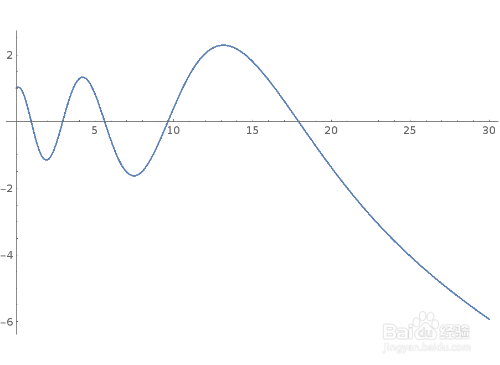
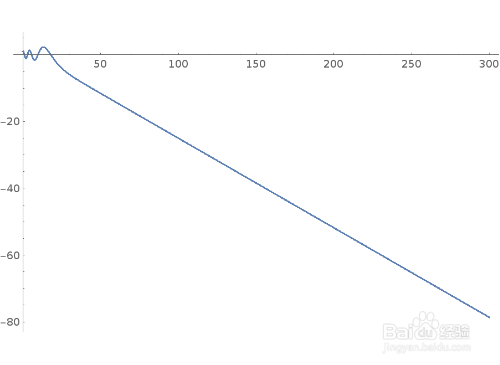
4、这个微分系统有两个显式解：

{y'[x]^2 == x - x^3, y[0] == 1}

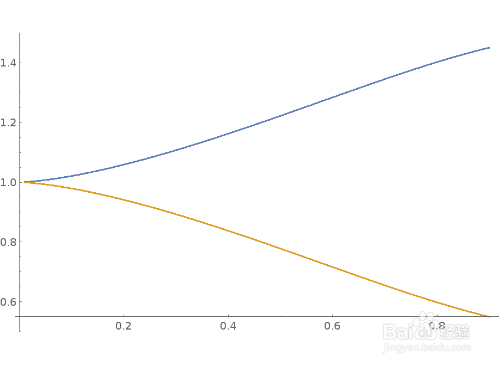
5、Mathematica竟然可以求出方程的隐式解。

y'[x]== -5 y[x]^2 - y[x]^3/x

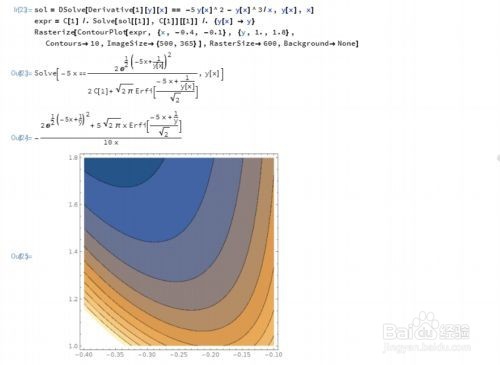
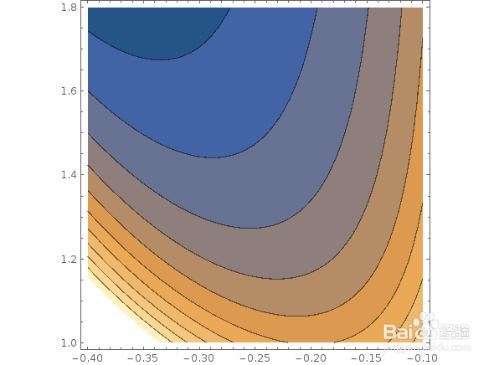
6、一个线性微分方程组：

{x'[t] + t*y[t] == 0, 2 y'[t] - 3 x[t] == 0, x[0] == 1, y[0] == 3}

可以分别绘制x[t]和y[t]的函数图形。

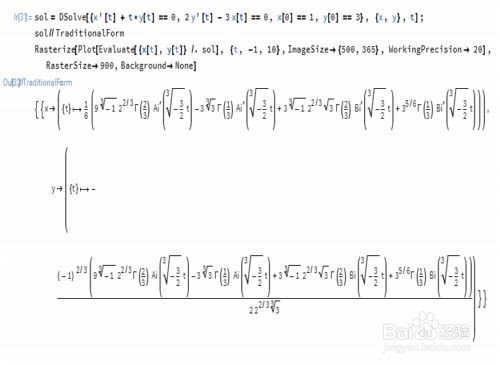
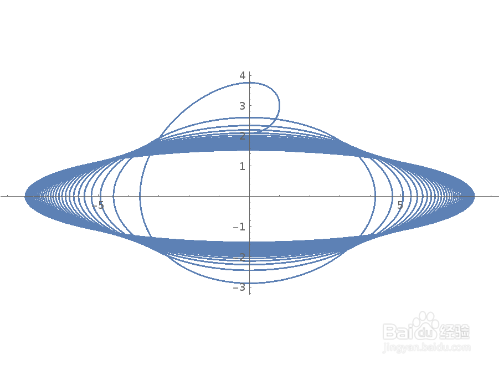
7、还可以把{x[t], y[t]}作为参数方程来对待。