【微分几何】圆环面上的迪潘指标线可视化
1、圆环面的参数方程是:
r = {(2 + Cos[u]) Cos[v], (2 + Cos[u]) Sin[v], Sin[u]};
为了便于计算迪潘指标线,先做一些准备工作。
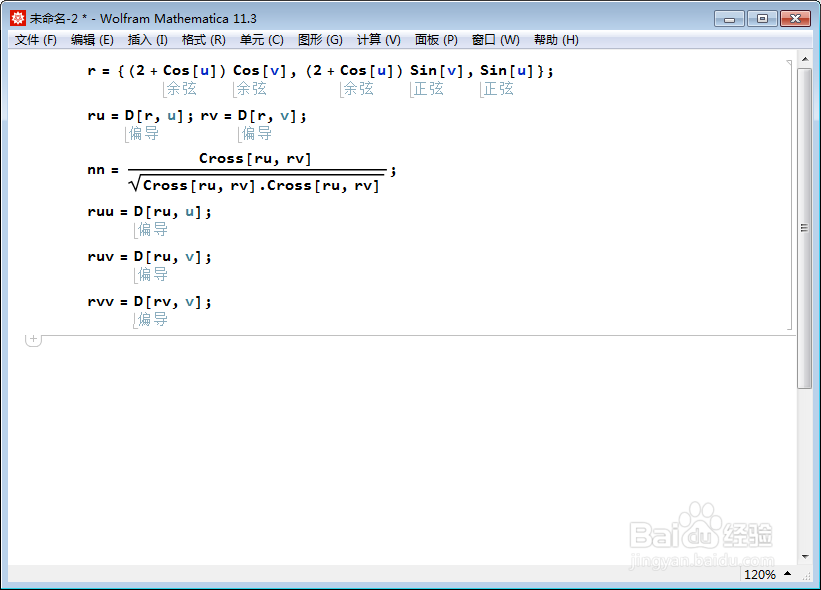
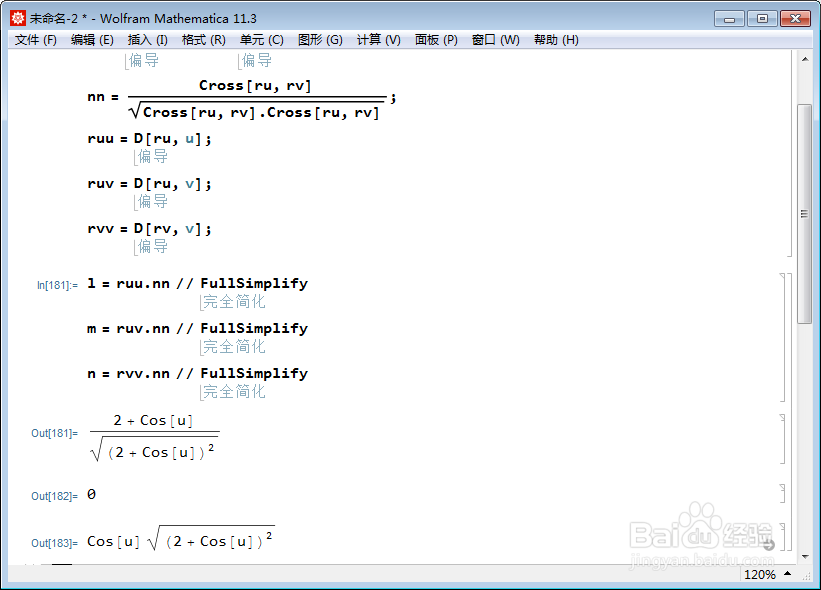
2、再计算曲面的第二基本量:
l = ruu.nn // FullSimplify
m = ruv.nn // FullSimplify
n = rvv.nn // FullSimplify
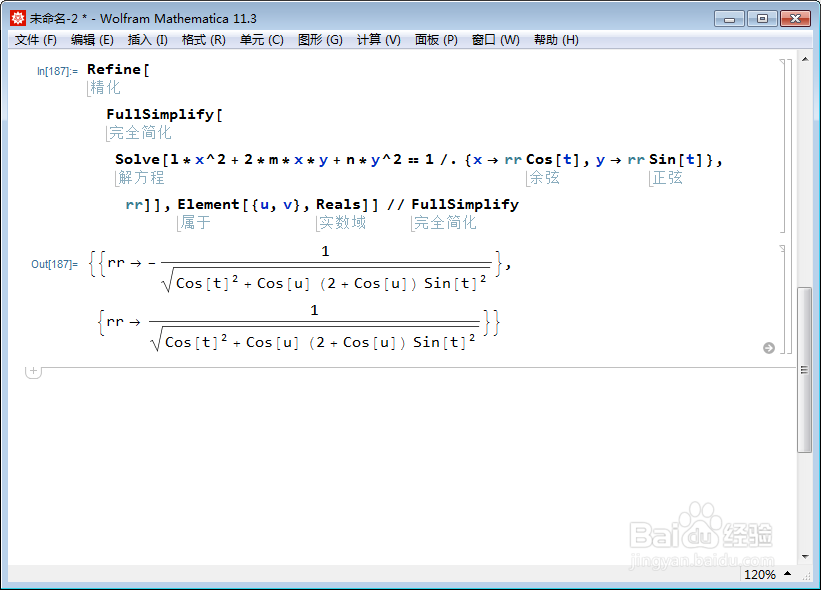
3、这样,就可以写出迪潘指标线的标准方程式。
如果以圆环面上的某个点A为原点、过点A的u曲线和v曲线的切线为x轴和y轴,那么迪潘指标线就在这个点的切平面上,其方程式是:
|l*x^2+2*m*x*y+n*y^2|=1
这容易求出其极坐标方程和参数方程:
Solve[l*x^2 + 2*m*x*y + n*y^2 == 1 /. {x -> rr Cos[t], y -> rr Sin[t]}, rr] // FullSimplify
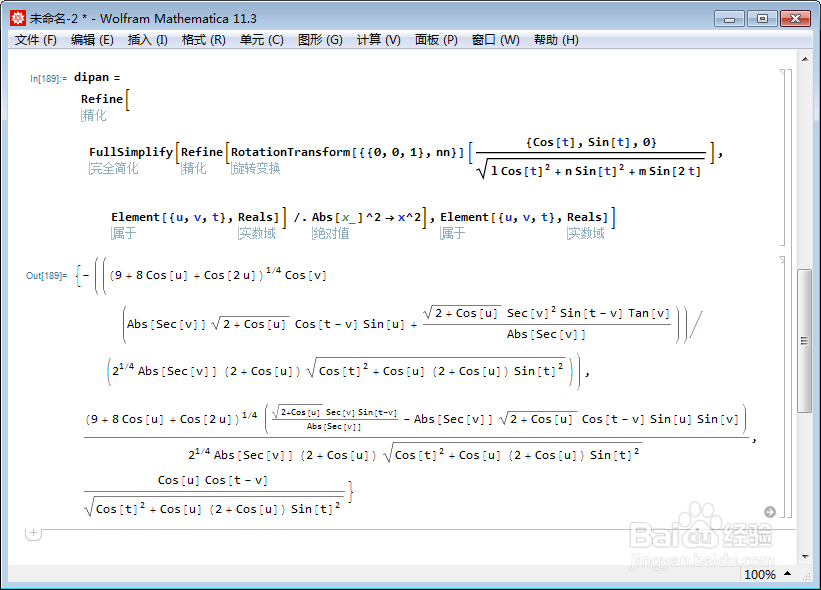
4、再经过旋转和平移操作,就可以得到原坐标系下,迪潘指标线的参数方程。
1、若A点在圆环面上的曲纹坐标是{0,0},那么其直角坐标是{3, 0, 0},此时的迪潘指标线如下图的蓝色椭圆。
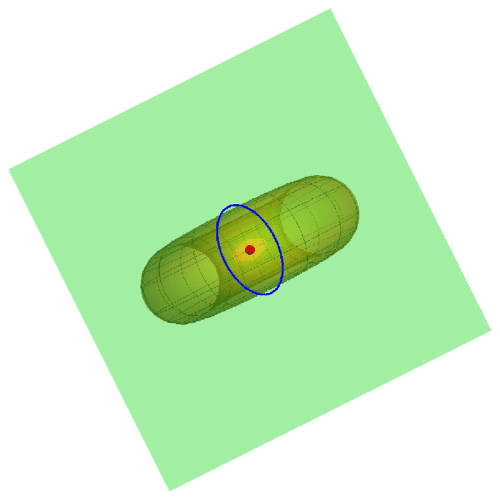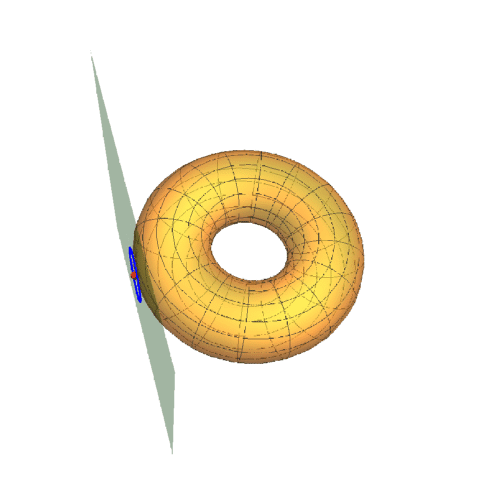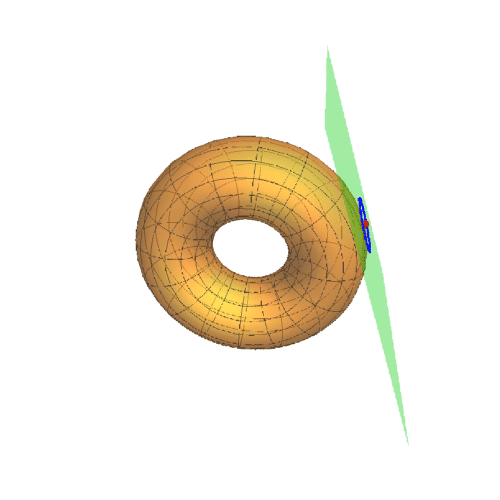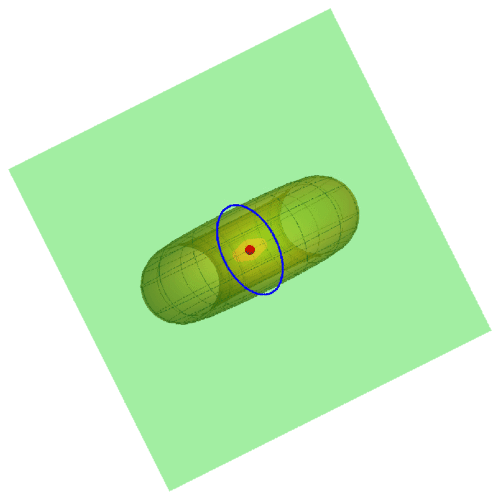
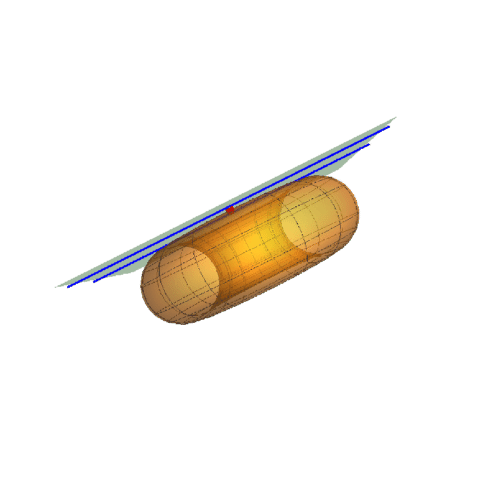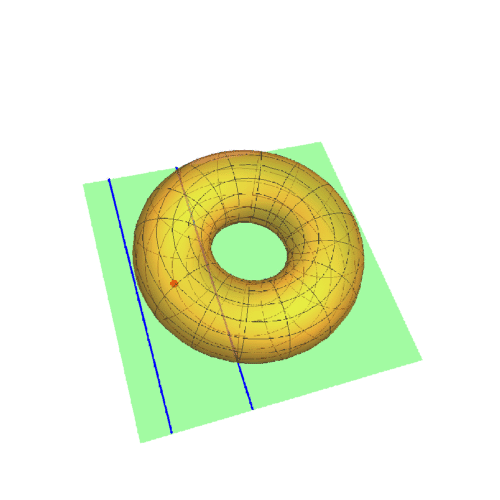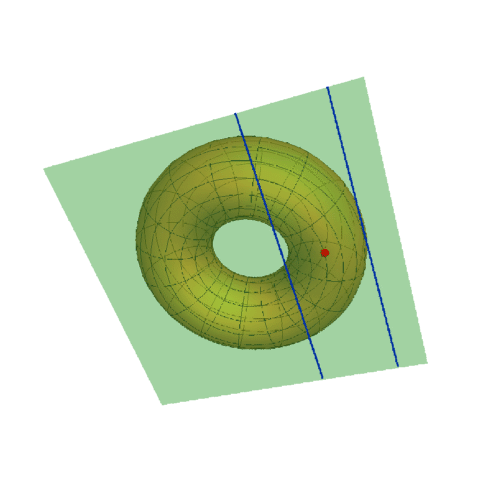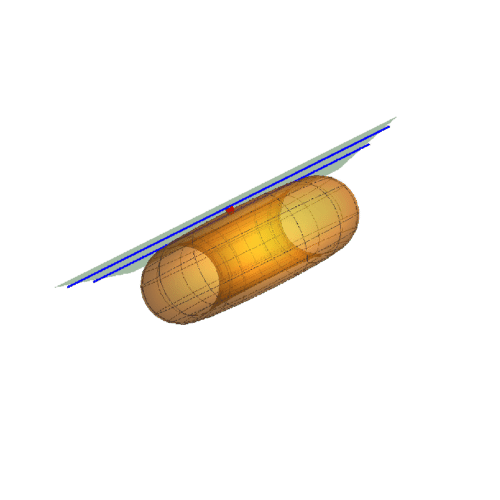
2、下面更换A的曲纹坐标,u的值改变,v的值保持为0。
A={Pi/2,0}
此时的迪潘指标线是两条平行线。
3、A={Pi,0}
此时迪潘指标线是双曲线。
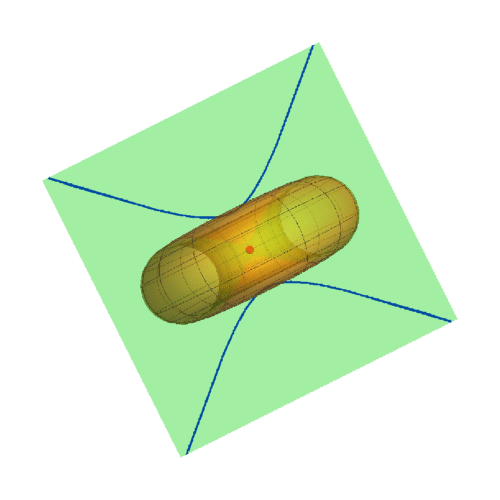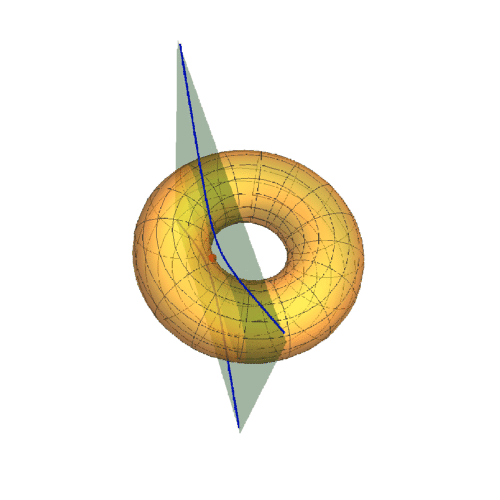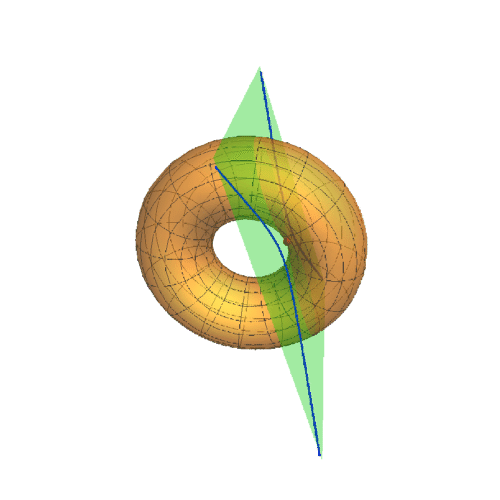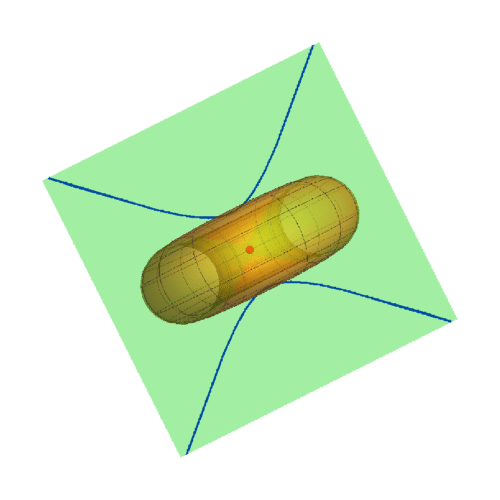
4、随着u的变化,考察迪潘指标线的变化。
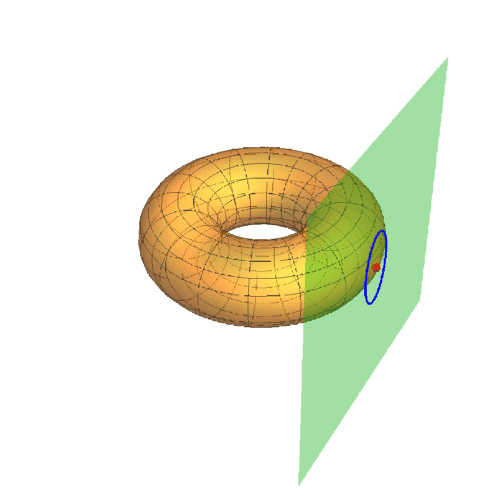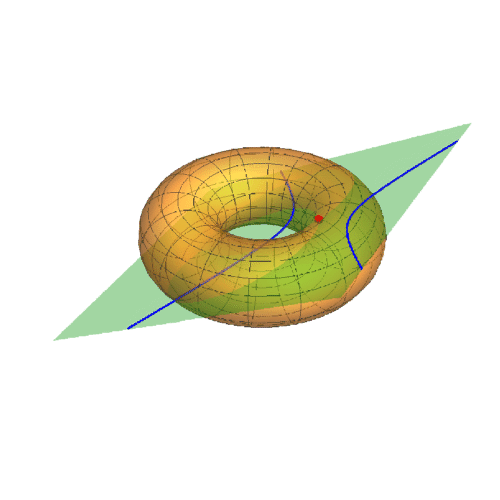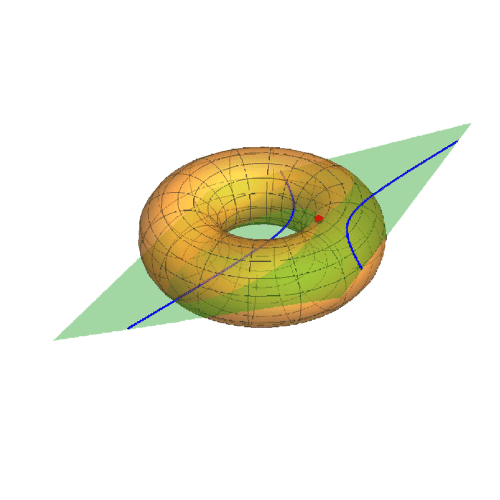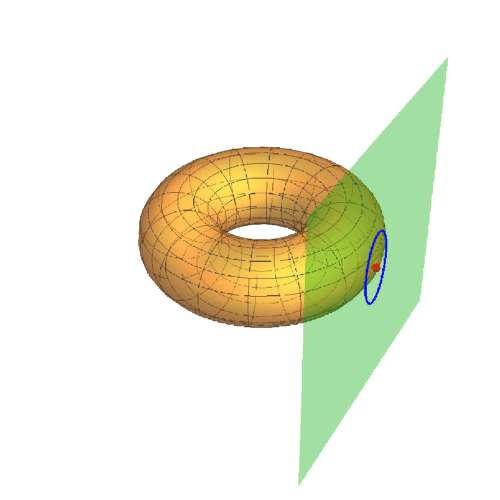
声明:本网站引用、摘录或转载内容仅供网站访问者交流或参考,不代表本站立场,如存在版权或非法内容,请联系站长删除,联系邮箱:site.kefu@qq.com。
阅读量:27
阅读量:125
阅读量:73
阅读量:131
阅读量:54