matlab多项式分析

1、特定点数值求解

对于给定的多项式表达式，比如f(x),求特定点（x0)值，可以采用polyval函数。

% polyval

% y = x^5 + 4*x^3 + 2*x^2 + x + 1

p = [1 0 4 2 1 1];

y1 = polyval(p,1)

其中，在表达多项式时，其实只需要表示出各项系数。计算结果如下所示：

2、多项式相乘

对于给定的多项式p1与p2，可以利用conv函数快速求解其乘积值：

% conv

% y1 = x^5 + 4*x^3 + 2*x^2 + x + 1

% y2 = x^2 + 4*x + 2

p1 = [1 0 4 2 1 1];

p2 = [1 4 2];

p = conv(p1,p2)

其中输出结果如下：

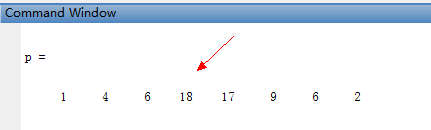
3、参数化显示多项式

在数学分析与书写时，我们习惯于参数化多项式，也就是含有变量的式子，可利用poly2str函数。

% poly2str

% y = 5*x^3 + 2*x + 3

p = [5 0 2 3];

ps = poly2str(p,'x')

4、根（零点）求解

在多项式分析时，常需要求解根，可使用roots指令。

% roots

% y = 5*x^4 + 4*x^2 + 2*x + 4

p = [5 0 4 2 4];

r = roots(p)

由于方程系数为4阶，可以求得4个实根。如下图所示：

5、多项式相除

有时候需要进行多项式之间除法，例如 p = p1 / p2 ，其中p1,p2为两个多项式，可以借助于deconv函数实现。

% roots

% y1 = 3*x^4 + 4*x^2 + 2*x + 6

% y2 = 5*x^2 + x + 3

p1 = [3 0 4 2 6];

p2 = [5 1 3];

[p,r] = deconv(p1,p2)

其中，p是相除后的商，而r为余数。