用Mathematica玩转一维元胞自动机

1、元胞自动机的函数是CellularAutomaton：

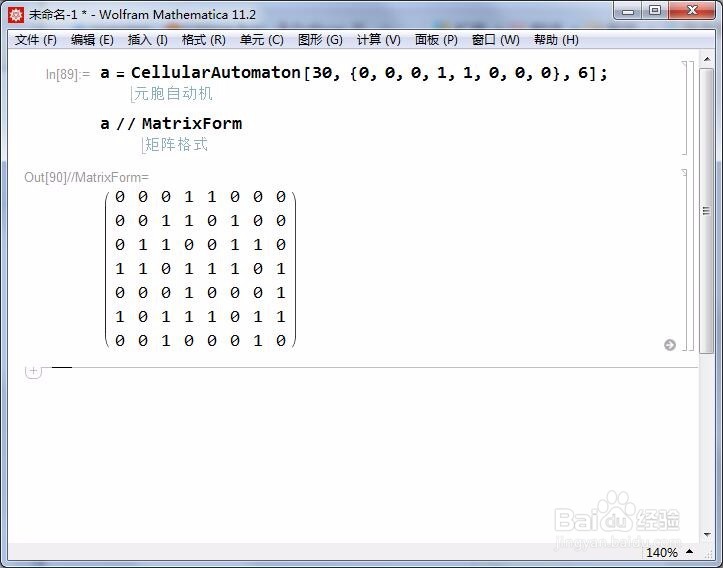
a = CellularAutomaton[30, {0, 0, 0, 1, 1, 0, 0, 0}, 6];

这是用规则30构造的元胞自动机；

初始状态是{0, 0, 0, 1, 1, 0, 0, 0}；

迭代了6次，得到了{0, 0, 1, 0, 0, 0, 1, 0}。

你能看出规则30的具体规则吗？

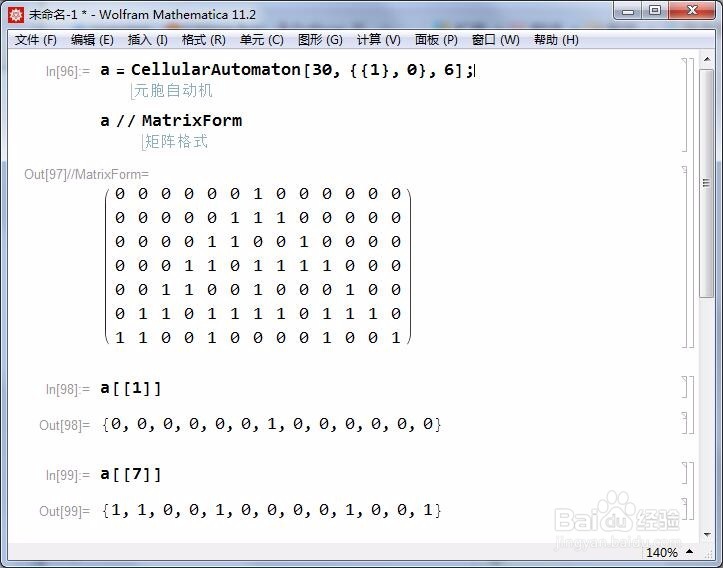
2、CellularAutomaton[30, {{1}, 0}, 6]

仍旧是规则30；

初始状态只有一个元胞，其余的全是0；

这个元胞在一维方向上分裂演化；

演化六次，得到{1, 1, 0, 0, 1, 0, 0, 0, 0, 1, 0, 0, 1}。

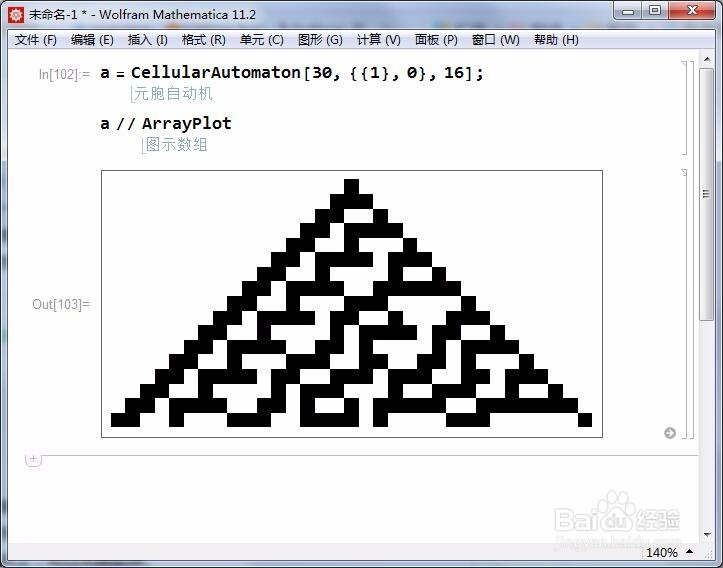
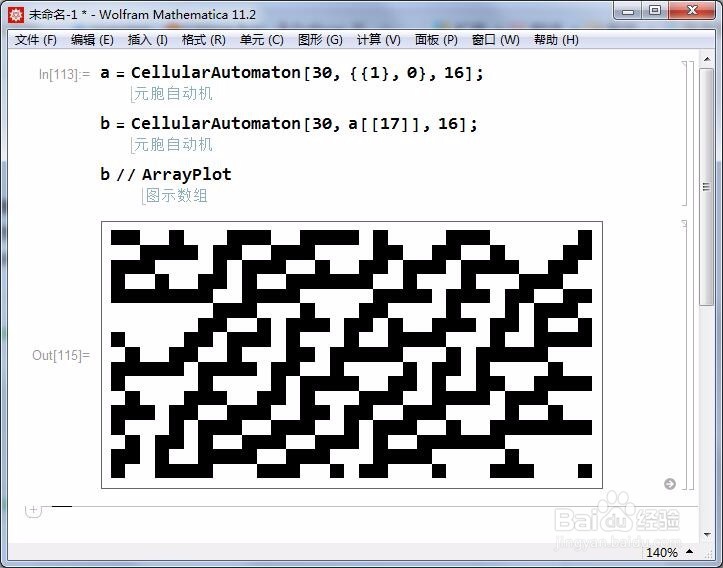
3、步骤1和步骤2都是一维的元胞自动机，却不相同：

前者的范围受到限制，只有8个位置供元胞自动机进行演化，触边即消；

后者在一维方向上，可以无限延伸。

4、把元胞自动机的演化过程，画成彩色的像素图：

ColorRules -> {1 -> Blue, 0 -> Lighter@Lighter@Lighter@Orange}

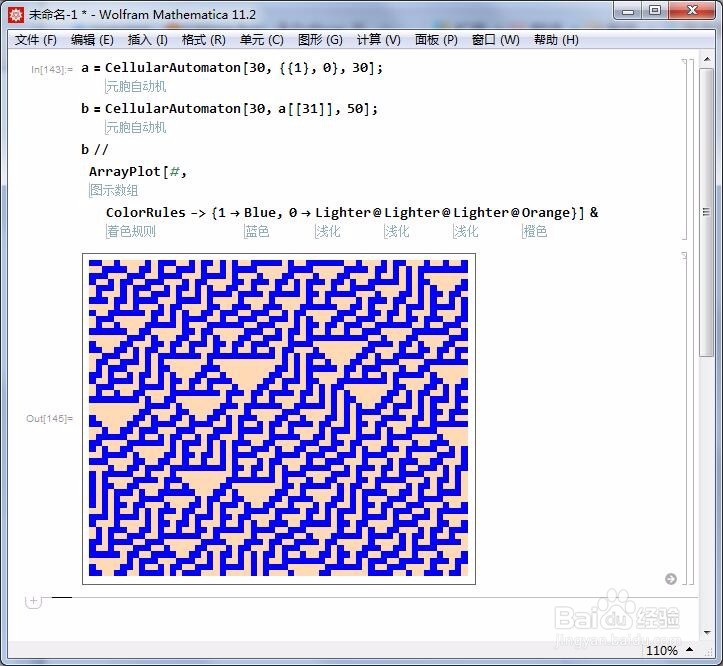
5、使用规则26，和一个一维元胞。

6、使用规则13，和一个一维元胞。

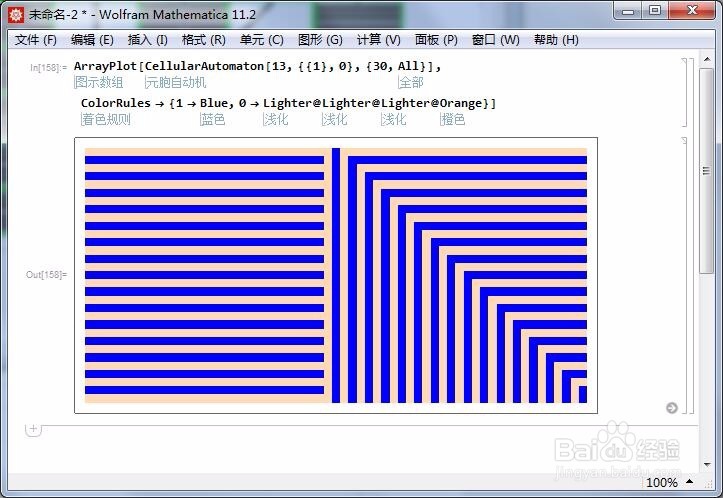
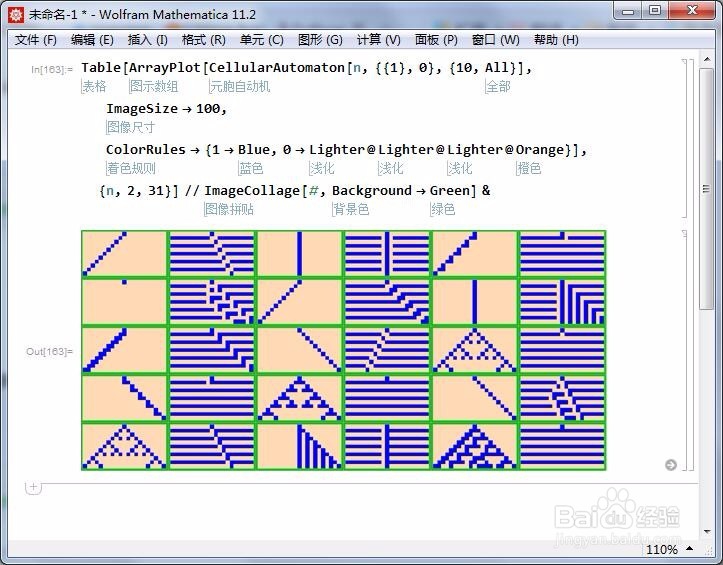
7、下图包括了规则2到规则31的像素图。