考研高数：极限有哪些运算法则？

1、两个（有限个）无穷小的和是无穷小，

可以想像一下，无穷小的极限是0，

那么0+0=0，所以同样的无穷小的和，最后也是趋向于0，

就是一个无穷小。

所以使用归纳法可以证明，有限个的无穷小的和也是无穷小。

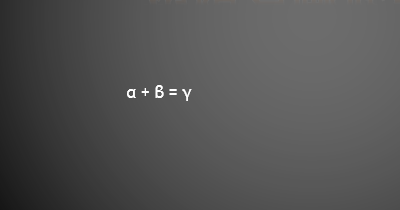
2、有界函数乘以无穷小是无穷小，

可以想像一下，无穷小的极限是0，

那么0*N=0，

公式为

uα=ε

u 为常数

3、如果两个函数的极限是常数A和B，

那么就可以加减乘除，

除法的时候，例如A/B，那么B不能为0.

4、如果两个数列的极限是常数A和B，

那么同样的也可以加减乘除，

除法的时候，例如A/B，那么B不能为0.

5、判断极限大小

如果两个函数φ(x) >=ψ(x),

两个对应的极限A和B的关系也是A>=B. 

6、复合函数的极限，

例如y=f(g(x))这个复合函数，

那么其对应的函数f(u) 和g(x)在x=x0的时候，对应的u0=g(x0)

有极限，那么符合函数也就有极限

这个也很好理解