Mathematica基础——不定方程问题

1、求不定方程x^2 - y^3 == 1所有的整数解：

Reduce[x^2 - y^3 == 1, {x, y},Integers]

答案是：（-3，2）、（-1，0）、（1，0）、（3，2）。不知道Mathematica为什么忽略了（-1，0）这组解！

2、Reduce在解一元三次方程的时候，不会给出根式解。

Reduce[x^3 + 2 x^2 + 3 x + 4 == 0, x]

需要根式解的话，需要Cubics（三次显式）加以限制：

Reduce[x^3 + 2 x^2 + 3 x + 4 == 0, x, Cubics -> True]

不如直接用Solve：

Solve[x^3 + 2 x^2 + 3 x + 4 == 0, x]

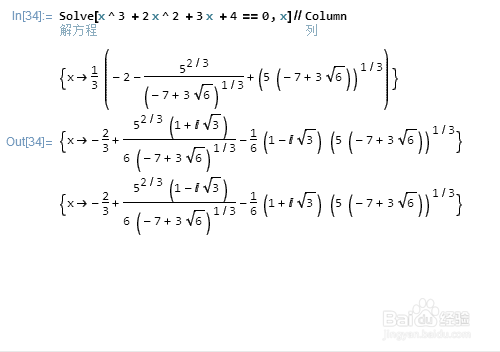
3、用面值为1元、2元、5元的货币，来购买17元的商品，可以有多少组合方法？

Reduce[a 1 + b 2 + c 5 == 17 && a >= 0 && b >= 0 && c >= 0, {a, b, c}, Integers]；

Length[%]

答案是：22.

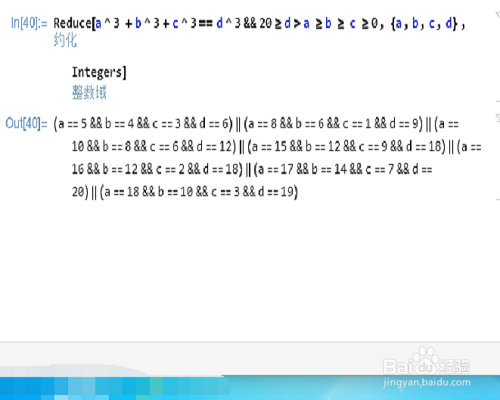
4、求不定方程a^3 + b^3+ c^3==d^3在d＜20的所有正整数解，但是具体条件有所松动：

Reduce[a^3 + b^3+ c^3==d^3&&20>= d>a >= b >=  c >= 0, {a, b, c,d}, Integers]

5、求解佩尔方程x^2 - 7 y^2 == 1 的通解：

Reduce[x^2 - 7 y^2 == 1 && x > 0 && y > 0, {x, y}, Integers]

还可以求该方程在1000以内的所有正整数解（估计不会多于100个）：

FindInstance[x^2 - 7 y^2 == 1 &&1000> x > 0 && 1000>y > 0, {x, y}, Integers,100]

事实上，只有两个！