怎么能够全面地认识12阶有限群？

1、Mathematica内置的12阶有限群，一共有13个。

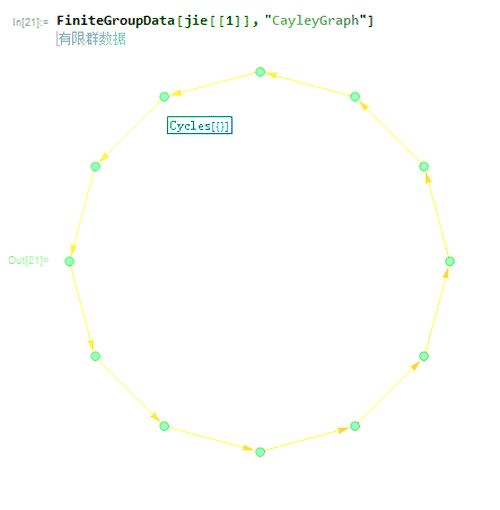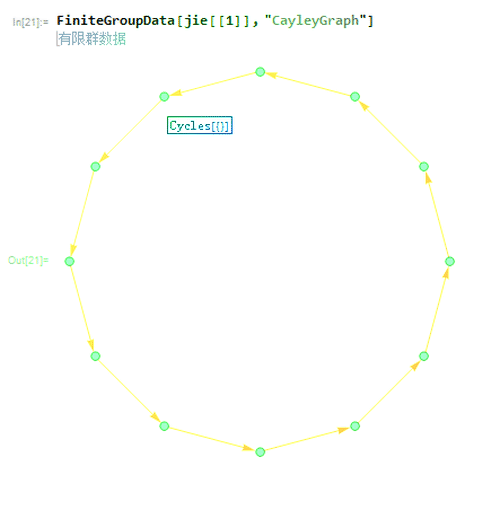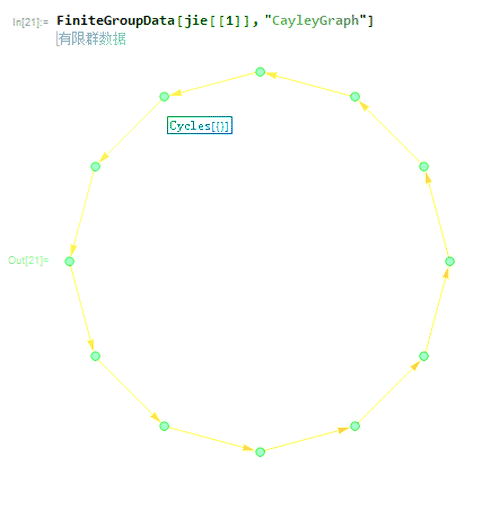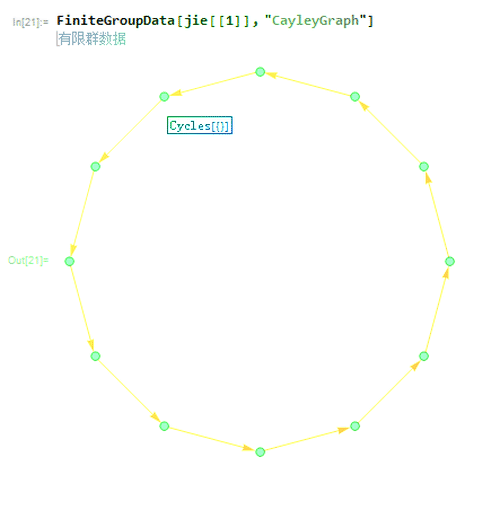
2、第一种就是{{"AbelianGroup", {4, 3}}；

对应的Caley图如下。

这是一个循环群，包含一个3阶子群和一个4阶子群。

3、第二种是{"AbelianGroup", {3, 2, 2}}，有一个3阶子群和两个2阶子群。

Caley如下图。

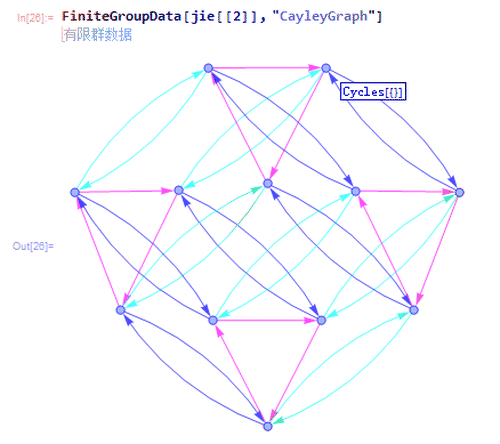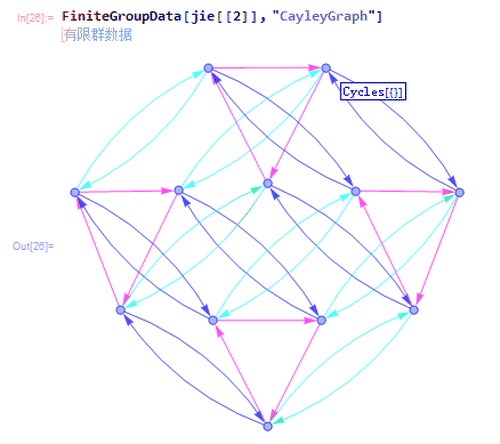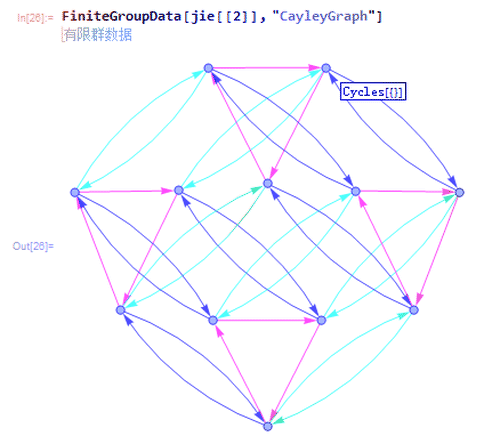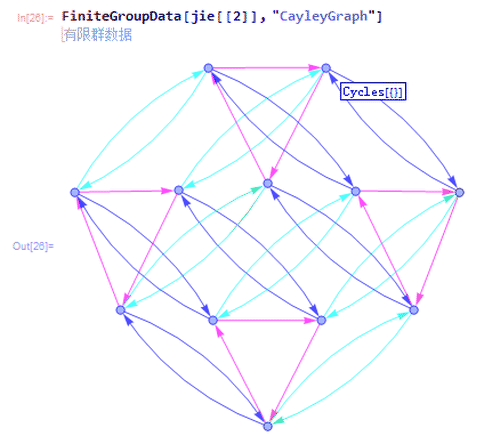
4、第三种是{"AlternatingGroup", 4}，也就是4阶交错群。

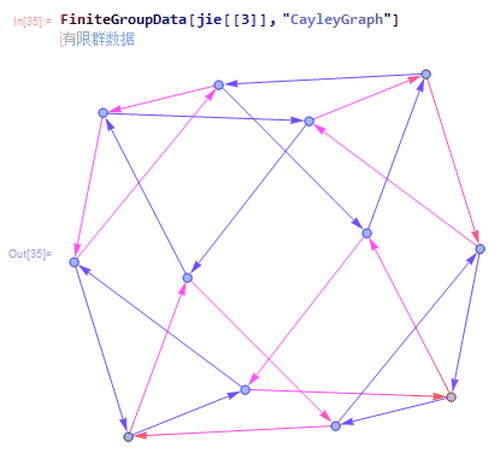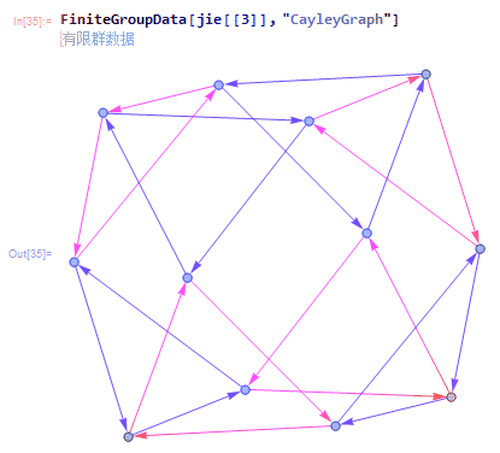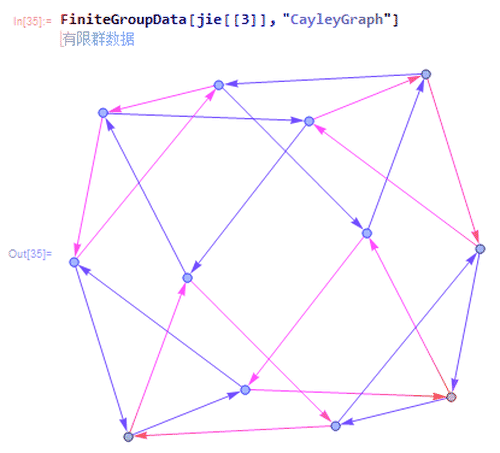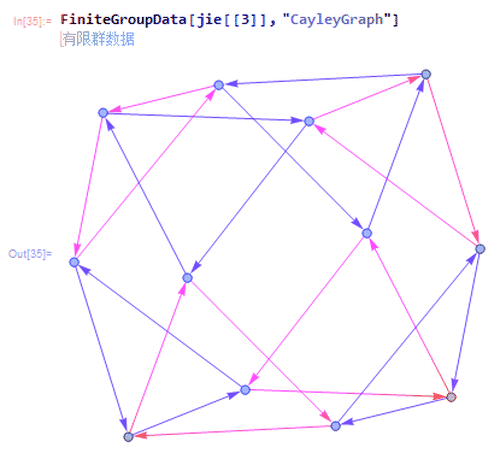
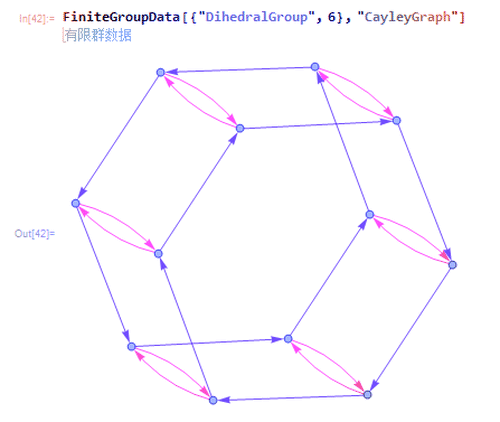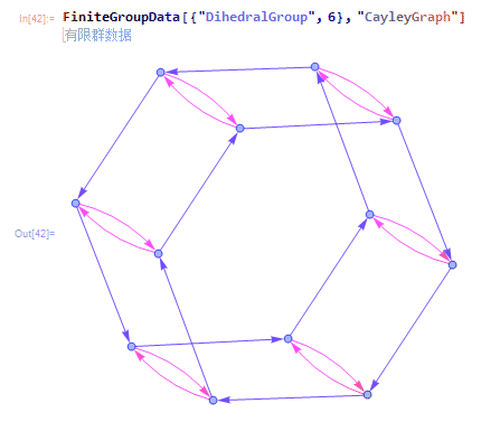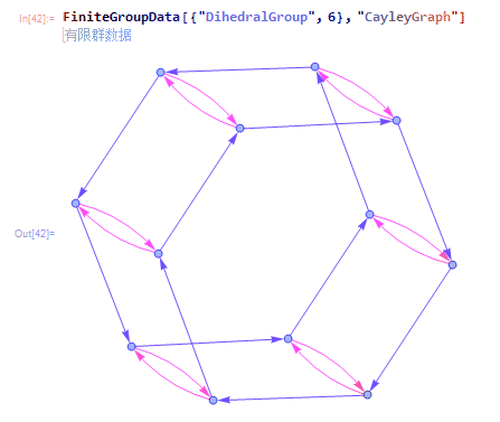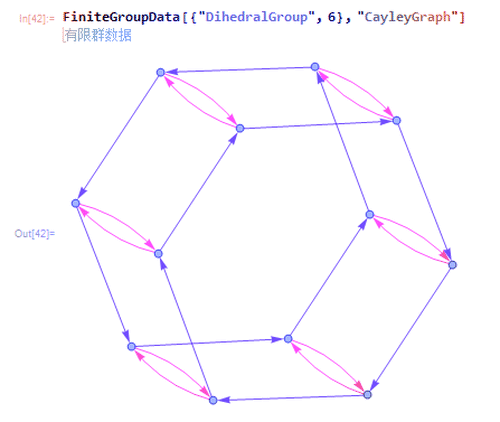
5、第11种是{"DihedralGroup", 6}，也就是二面体群D6。

6、双环群——{"DicyclicGroup", 3}——排在第10个位置上。

7、这五种12阶群，代表了五种同构类。

任何一个12阶群，都和上面某一个同构。

这通过它们的Caley可以看出来。

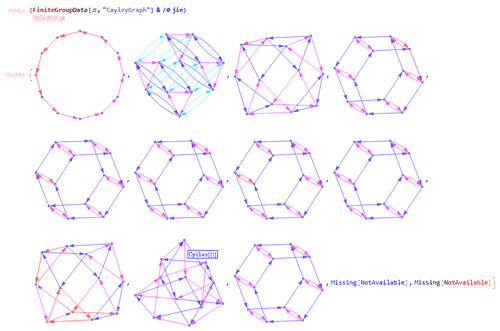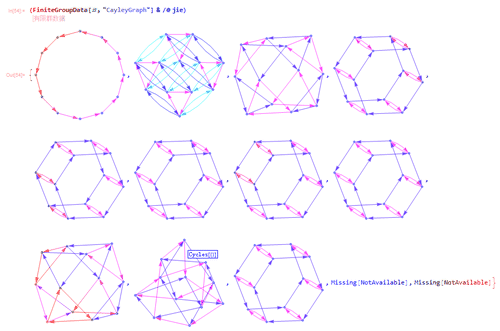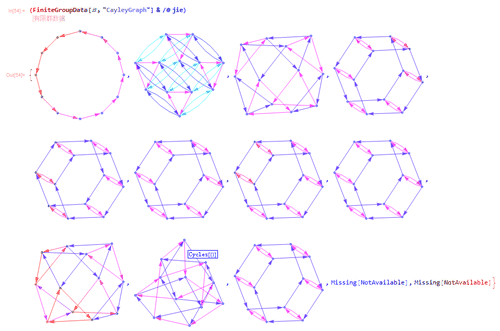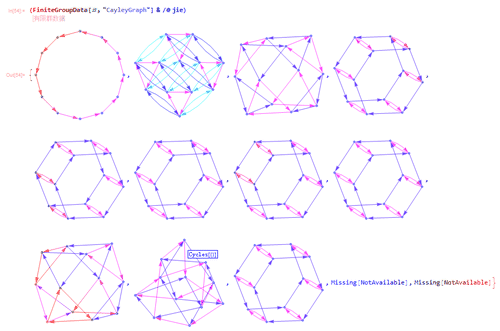
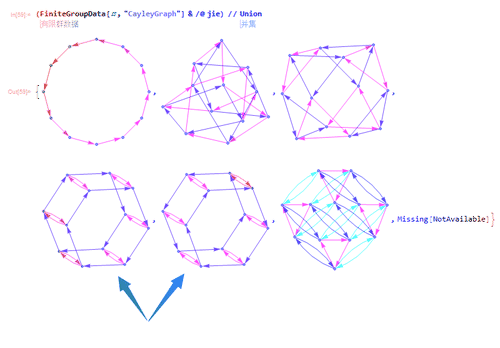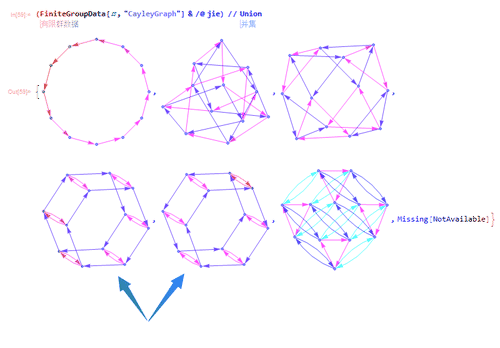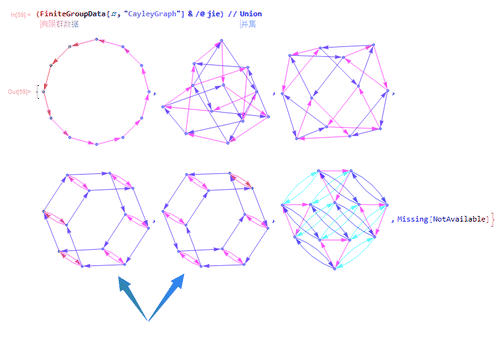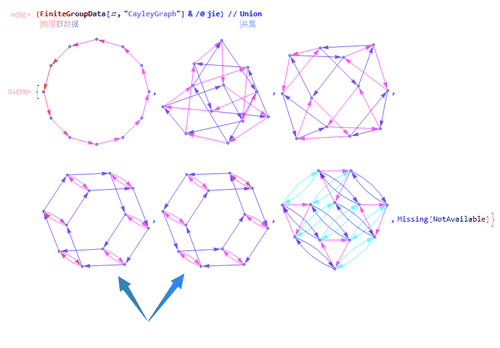
8、除了最后两个没画出图来，其余的，用Union处理一下，就只剩下6个图；

这六个图还有两个图本质上是同一个图，因此，只有五大类。