【Mathematica】微分方程组的数值解法

1、要求解的方程组是：

{x'[t] + y[t]^2 == 1, y'[t] + x[t]^2 == 2}

初始条件是：

x[1] == 1, y[1] == 2

直接用DSolve，计算机将进入某种奇异状态：

DSolve[{x'[t]+y[t]^2==1,y'[t]+x[t]^2==2,x[1]==1,y[1]==2}, {x[t], y[t]}, t]

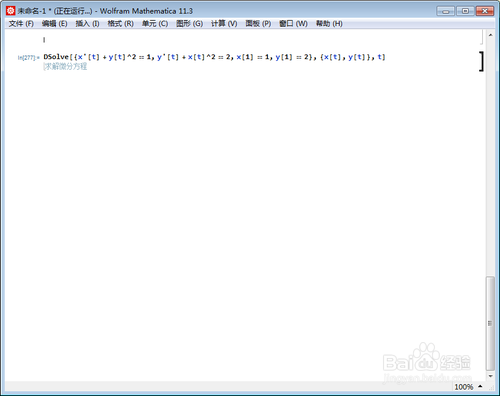
2、由于DSolve长时间算不出结果，就直接套用NDSolve计算数值解：

NDSolve[{x'[t]+y[t]^2==1,y'[t]+x[t]^2==2,x[1]==1,y[1]==2}, {x[t], y[t]}, t]

这时候会报错。

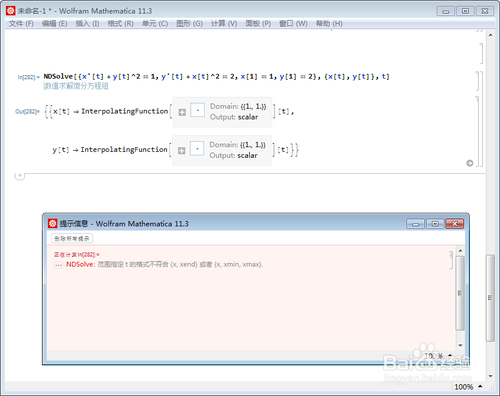
3、NDSolve[{x'[t]+y[t]^2==1,y'[t]+x[t]^2==2,x[1]==1,y[1]==2}, {x[t], y[t]}, 

            {t,-10,10}]

给t制定一个取值范围，仍旧报错。这是因为这个范围内，很可能遇到了微分方程系统的奇异值。

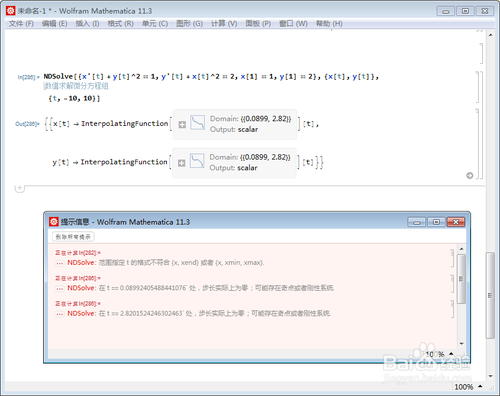
4、重新调整t的范围，把可能存在的奇异值排除掉：

NDSolve[{x'[t]+y[t]^2==1,y'[t]+x[t]^2==2,x[1]==1,y[1]==2}, {x[t], y[t]}, 

            {t,0.09,2.8}]

运行，不再报错。

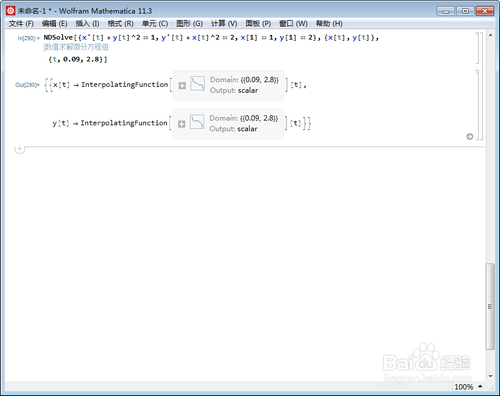
5、出来结果，就可以画图了：

ParametricPlot[{x[t], y[t]} /. sol, {t, 1, 2}]

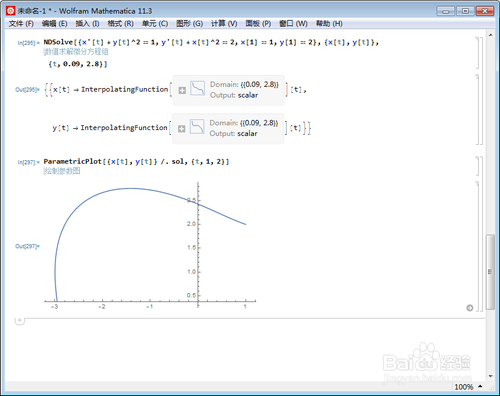
6、画图范围一定不要超出解方程组的时候所预定的t的取值范围：

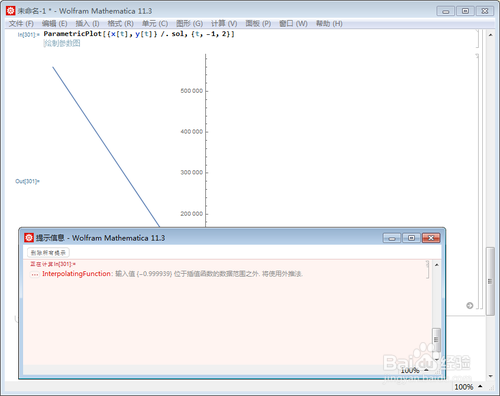
7、有时候即便不出界，也会报错，

不知道为什么数值解可以求出来，图像却不可作。

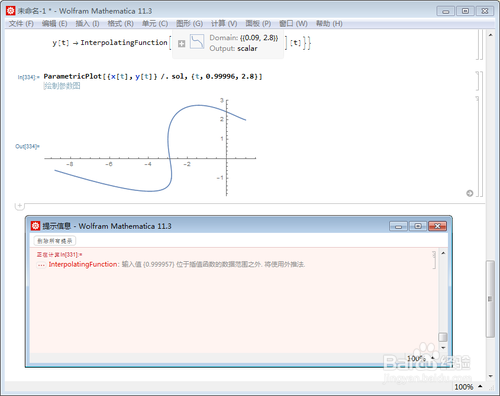
8、一直调整到0.99995，还是报错，直到0.99996，才可以正常作图。