Mathematica基础——解微分方程并作图
1、qi求解微分方程y'[x] == x^2*Sin[x] + Sqrt[1 + x^2]。

2、解微分方程y'[x] == -(x^2 - 3 y[x]^2)/(x*y[x])。
这个方程有一个隐函数解,但是Mathematica给出了两支显式解。
这可能是Mathematica的一个不足。
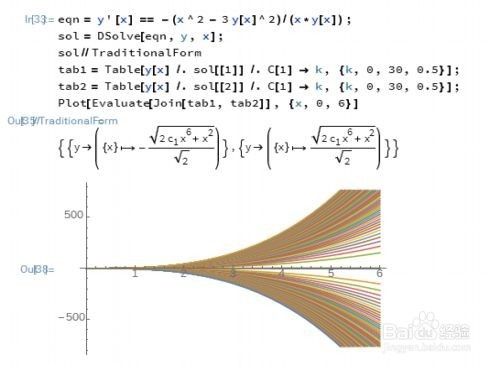
3、求解一个全微分方程:
P[x_, y_] := -(5 x^2 - 2 y^2 + 11)Q[x_, y_] := (Sin[y] + 4 x*y + 3)eqn = y'[x] == -P[x, y[x]]/Q[x, y[x]]


4、求解Clairaut方程:
y[x] == x*y'[x] + y'[x]^2 + Exp[y'[x]]
它的通解是一族直线。


5、求解一个二阶非齐次线性方程:
x^2 y''[x] + y[x] == x^2
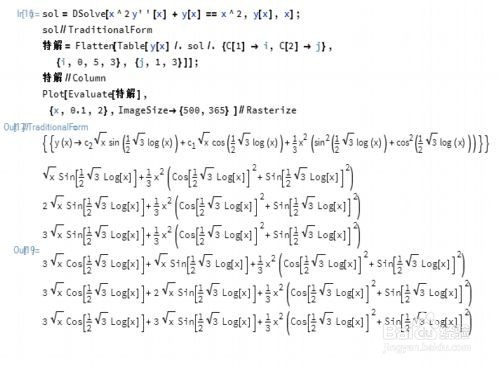

声明:本网站引用、摘录或转载内容仅供网站访问者交流或参考,不代表本站立场,如存在版权或非法内容,请联系站长删除,联系邮箱:site.kefu@qq.com。
阅读量:178
阅读量:45
阅读量:114
阅读量:104
阅读量:90