用Mathematica演示级数逼近的现象——幂级数

1、        先来求正弦函数sinx在x=0时的幂级数展开式，且使得级数式取到x^20项（20阶）：

Series[Sin[x], {x, 0, 20}]

2、        用列表的形式，把sinx的前20阶的幂级数展开式表示出来：

Table[Series[Sin[x], {x, 0, n}], {n, 1, 20}]

3、        如果感觉有点乱，可以用Column进行排列：

Table[Series[Sin[x], {x, 0, n}], {n, 1, 20}] // Column

        这样观察起来就容易多了！

4、        我们把sinx的前20阶幂级数的余项去掉，便于作图：

Table[Series[Sin[x], {x, 0, n}], {n, 1, 20}] // Column // Normal

Table[Series[Sin[x], {x, 0, n}], {n, 1, 20}] // Normal // Column

        大家可以比较一下上面两个代码运行之后的结果，看看有什么区别，并思考一下出现这种区别的原因！

5、        把sinx的前20阶幂级数的图像画出来，并与sinx的图像加以比较：

Plot[Evaluate[

  Table[Normal[Series[Sin[x], {x, 0, n}]], {n, 1, 20, 1}]], {x, 0, 

  4 Pi}, PlotRange -> 3]

        和

Plot[Evaluate[

  Table[Normal[Series[Sin[x], {x, 0, n}]], {n, 1, 20, 1}]], {x, 0, 

  4 Pi}, PlotRange -> 100]

        和

Plot[{Sin[x], 

  Evaluate[Table[

    Normal[Series[Sin[x，{x, 0, n}]], {n, 1, 20, 1}]]}, {x，0, 4 Pi},

  PlotRange -> 3]

        注意，当PlotRange取到100的时候，sinx的波动几乎就是看不着了！

6、        用动态图模拟这个逼近过程：

Manipulate[

 Plot[{Sin[x], Evaluate[Normal[Series[Sin[x], {x, 0, n}]]]}, {x, 0, 

   10 Pi}, PlotRange -> 2]， {n, 1, 20, 1}]

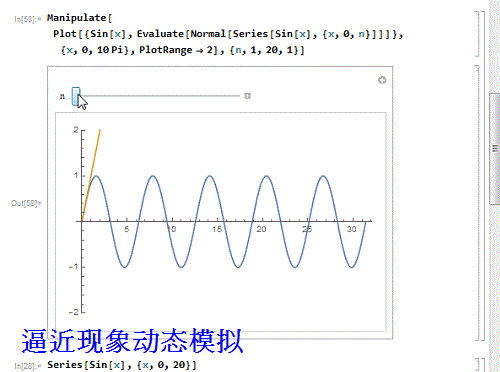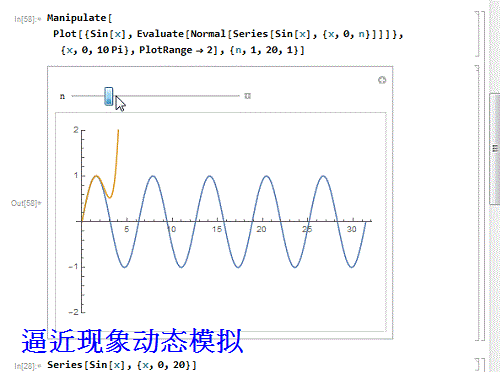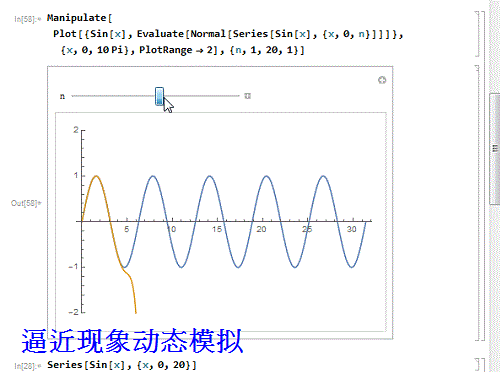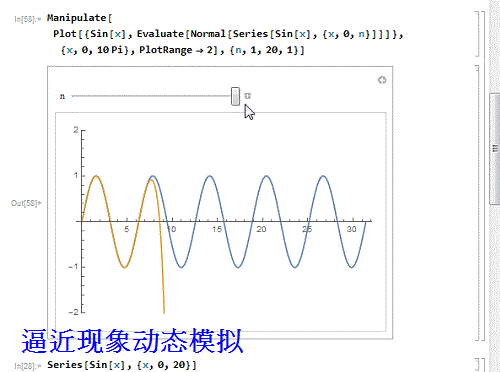
7、        感觉逼近的程度不够？那就要继续增加幂级数的阶数，100阶：

Manipulate[

 Plot[{Sin[X], Evaluate[NorMal[Series[Sin[x], {x, 0, n}]]]}, {x, 0, 

   10 Pi}, PlotRange -> 2], {n, 1, 100, 1}]

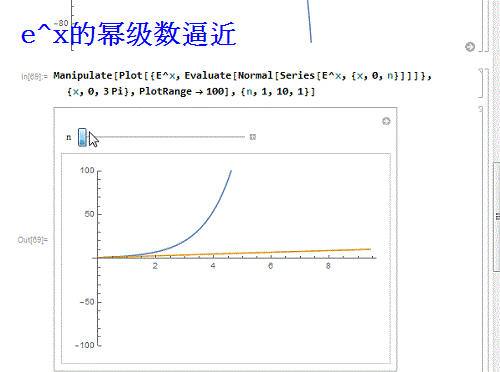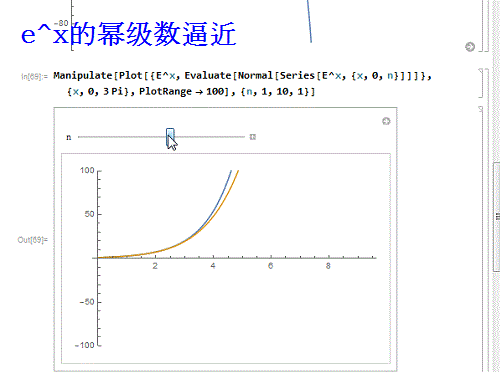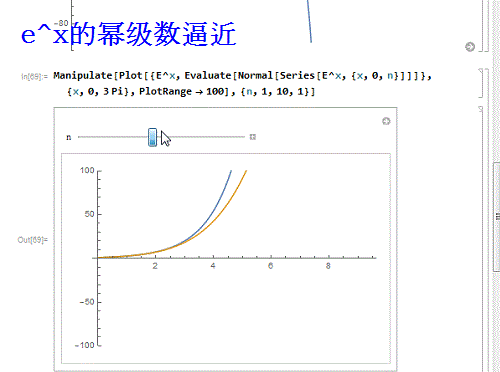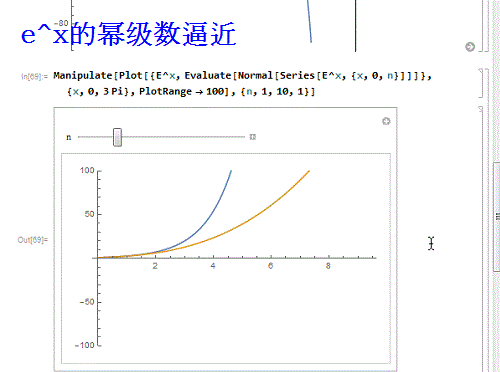
8、        再换一个函数——e^x：

Manipulate[

 Plot[{E^X， Evaluate[Normal[Series[E^x, {x, 0, n}]]]}, {x, 0, 3 Pi}, 

  PlotRange -> 100], {n, 1, 10, 1}]

        e^x和sinx有一个特点，就是它们的幂级数处处收敛！

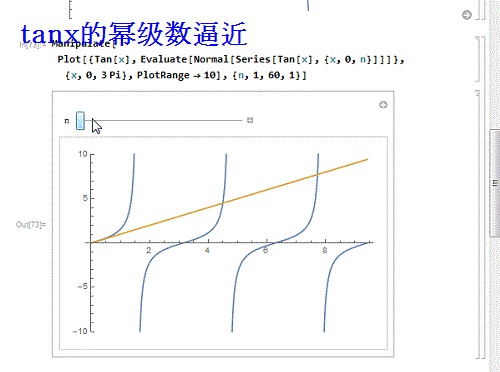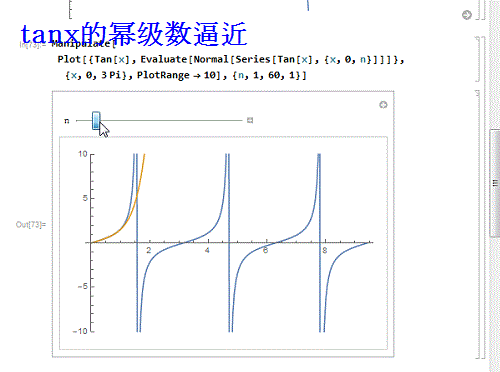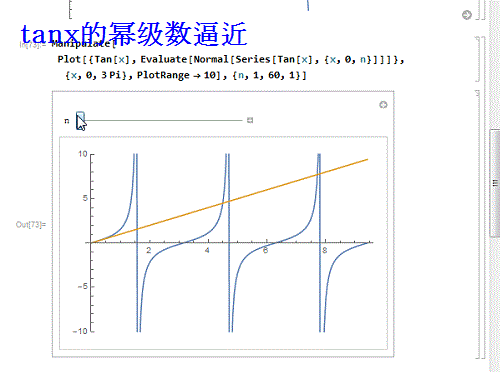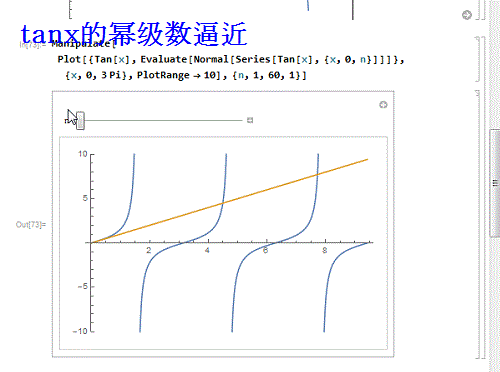
9、        如果换一个不能处处收敛的呢？比如tanx：

Manipulate[

 Plot[{Tan[x], Evaluate[Normal[Series[Tan[X], {x，0, n}]]]}, {x, 0, 

   3 Pi}, PlotRange -> 10], {n, 1, 60, 1}]

        发现，只有在收敛区间内，幂级数才能逼近函数！