函数y=√x(36x+80/x)的图像示意图

1、函数的定义域

∵√x有x≥0；对80/x有x≠0.

∴函数的定义域为：(0，+∞）。

2、∵y=√x(36x+80/x)

=36x^(3/2)+80x^(-1/2),对x求导得：

∴dy/dx

=(3/2)*36x^(1/2)-(80/2)x^(-3/2)

=(1/2)x^(-3/2)(3*36x²-80).

3、令dy/dx=0,则x²=20/27.

又因为x>0，则x=(2/9)√15≈0.86.

(1)当x∈(0, (2/9)√15)时，dy/dx＜0,函数y为单调减函数；

(2)当x∈[(2/9)√15,+∞)时，dy/dx＞0,函数y为单调增函数。

4、∵dy/dx=(1/2)x^(-3/2)(3*36x²-80)，

∴d^2y/dx^2

=-3/4*x^(-5/2)(3*36x²-80)+3*36x*x^(-3/2)

=-3/4*x^(-5/2)(3*36x²-80)+3*36x^(-1/2)

=-3/4x^(-5/2)(3*36x²-80-4*36x²)

=3/4x^(-5/2)(36x²+80)>0,则：

函数y在定义域上为凹函数。

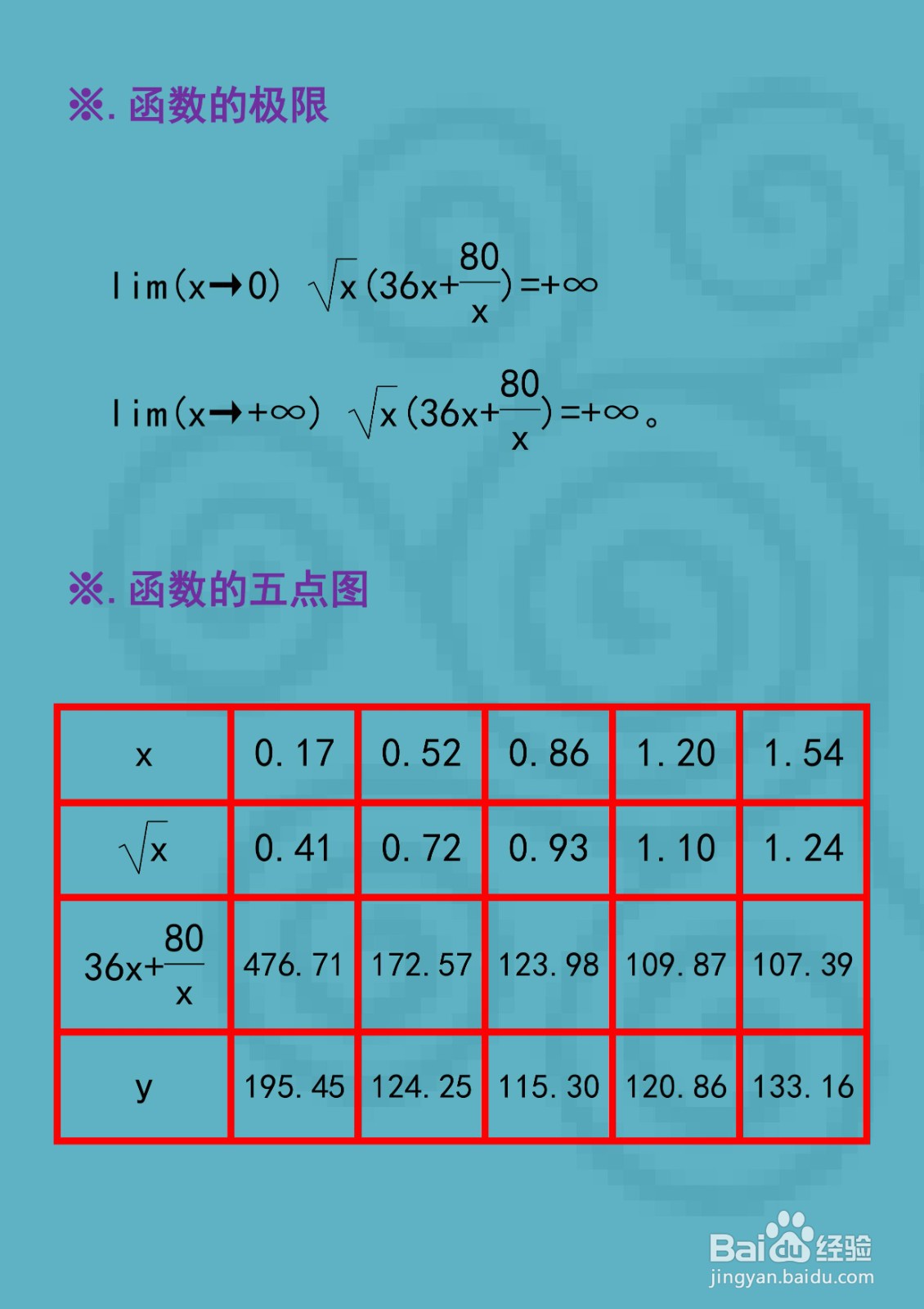
5、函数的极限及五点图表

Lim(x→0) √x(36x+80/x)=+∞

Lim(x→+∞) √x(36x+80/x)=+∞。

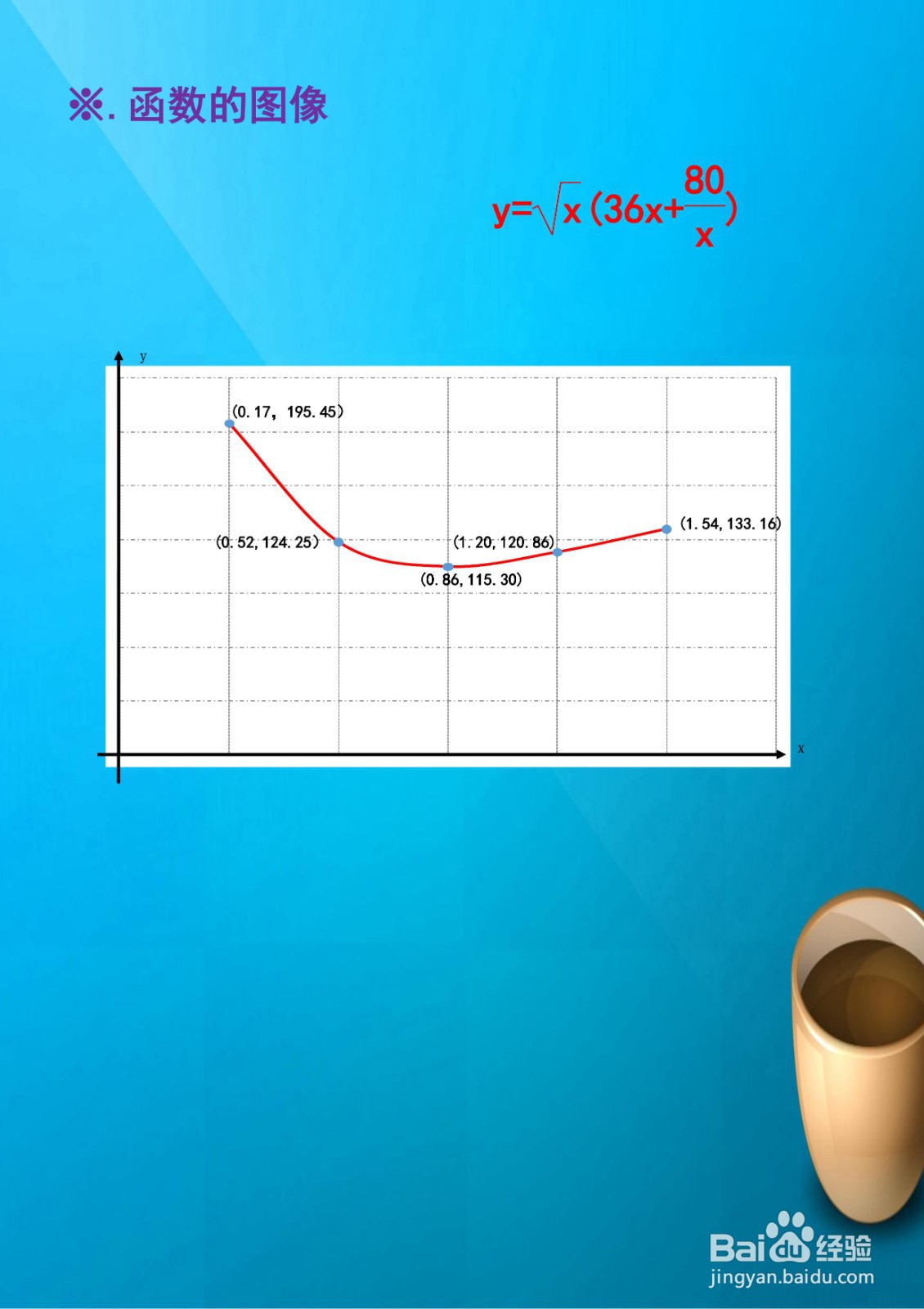
6、综合以上函数的性质，函数的示意图如下：