函数的一阶导数练习题及详细解析A2

1、例题:计算y=(35x-160)^(-1/2)导数

思路：幂函数的求导公式应用：

dy/dx=(-1/2)*(35x-160)^(-3/2)*35.

2、例题:函数y=(56-42x+28x³)7 导数计算步骤

 思路：幂函数的链式求导法则，具体过程为：

y'=7*(56-42x+28x³)6 *(56-42x+28x³)'

=7*(56-42x+28x³)6 *(-42+3*28x2).

3、例题:函数y=√(1+47x2)的导数计算  

因为：y=(1+47x2)^(1/2),进一步由幂函数求导公式有：

所以：y'=(1/2)*(1+47x2)^(-1/2)*2*47x

=47x*(1+47x2)^(-1/2).

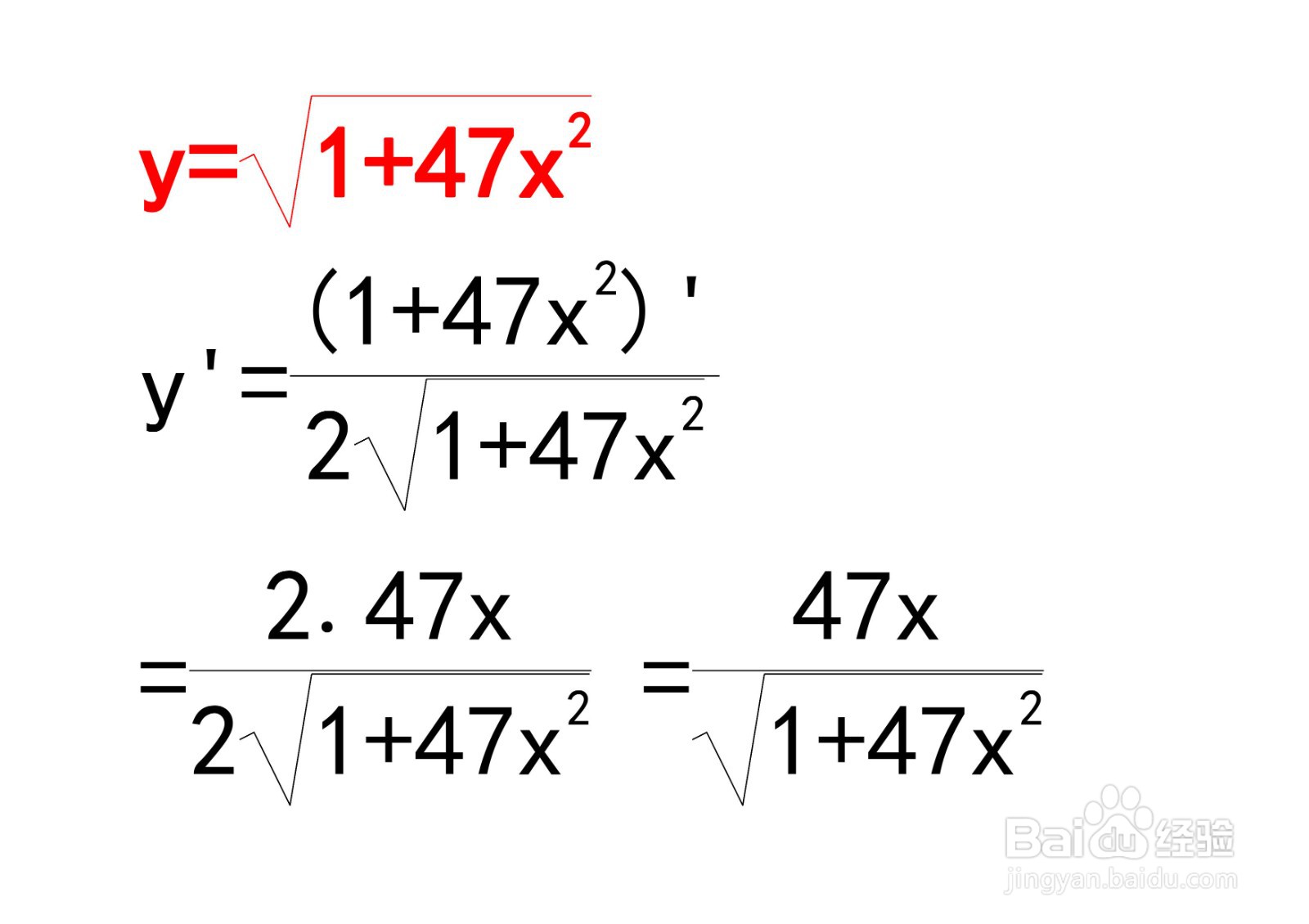
1、例题:计算y=ln(124x²+93) 导数

  思路：由对数的导数计算公式，求解函数的导数，即：

dy/dx=(124x²+93)'/(124x²+93)=248x/(124x²+93).

2、例题:计算y=15√x.ln9x 的导数   

思路：本题是幂函数和对数函数的乘积，用到函数乘积的求导法则以及幂函数和对数函数的求导，步骤为：y'=15[1/2.ln9x*(1/√x )+√x(9/9x)]=15(1/2.ln9x*(1/√x )+1/√x]

=15*(ln9x+2)/(2√x) 。   

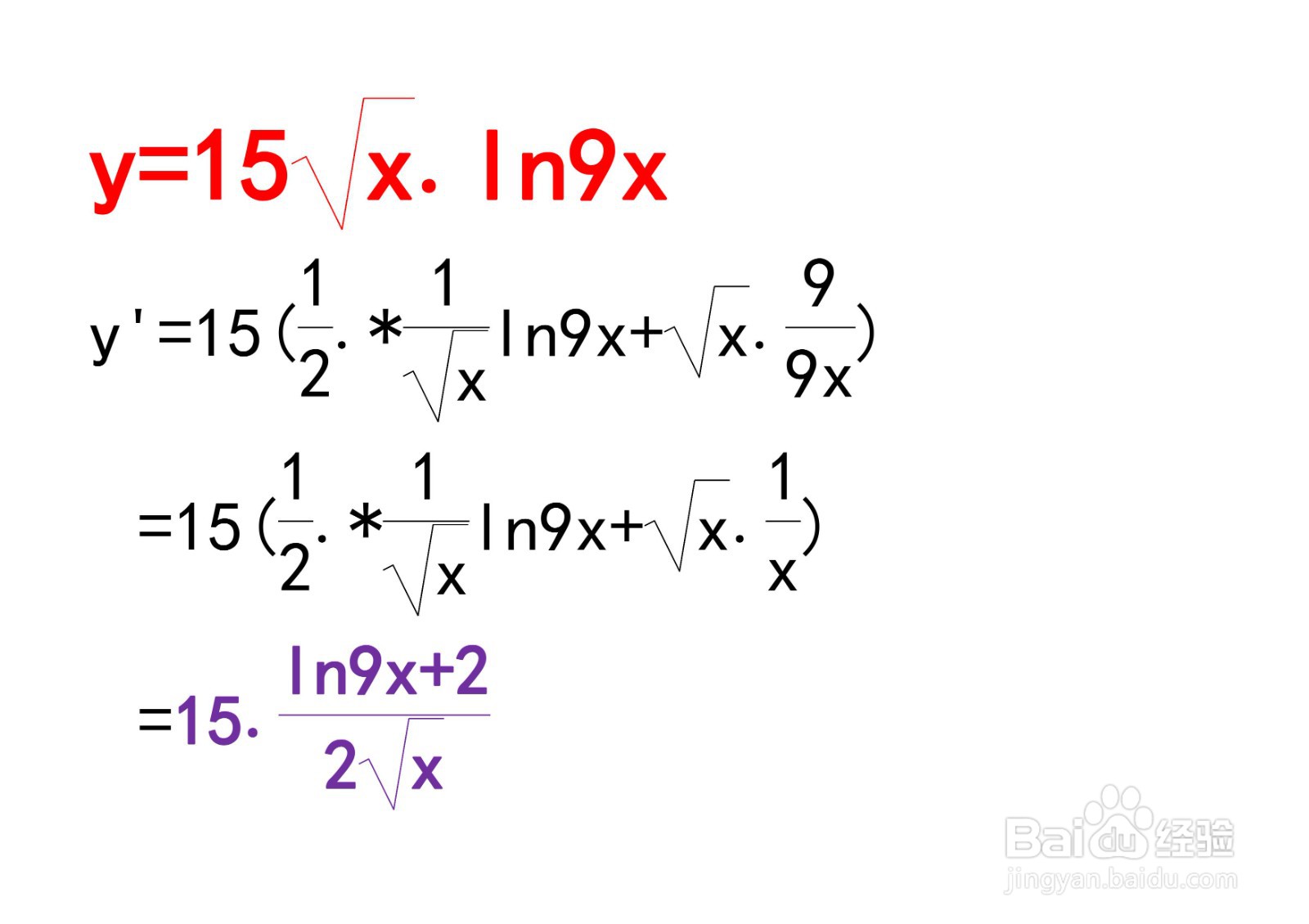
3、例题:计算y=(65-lnx)/(24+lnx)的导数

思路：本题是对数函数商的求导法则的应用，详细过程如下：

y'=[-1/x*(24+lnx)-(65-lnx)*(1/x)]/(24+lnx)²

=-1/x*[(24+lnx)+(65-lnx)]/(24+lnx)²

=-89/[x(24+lnx)²].

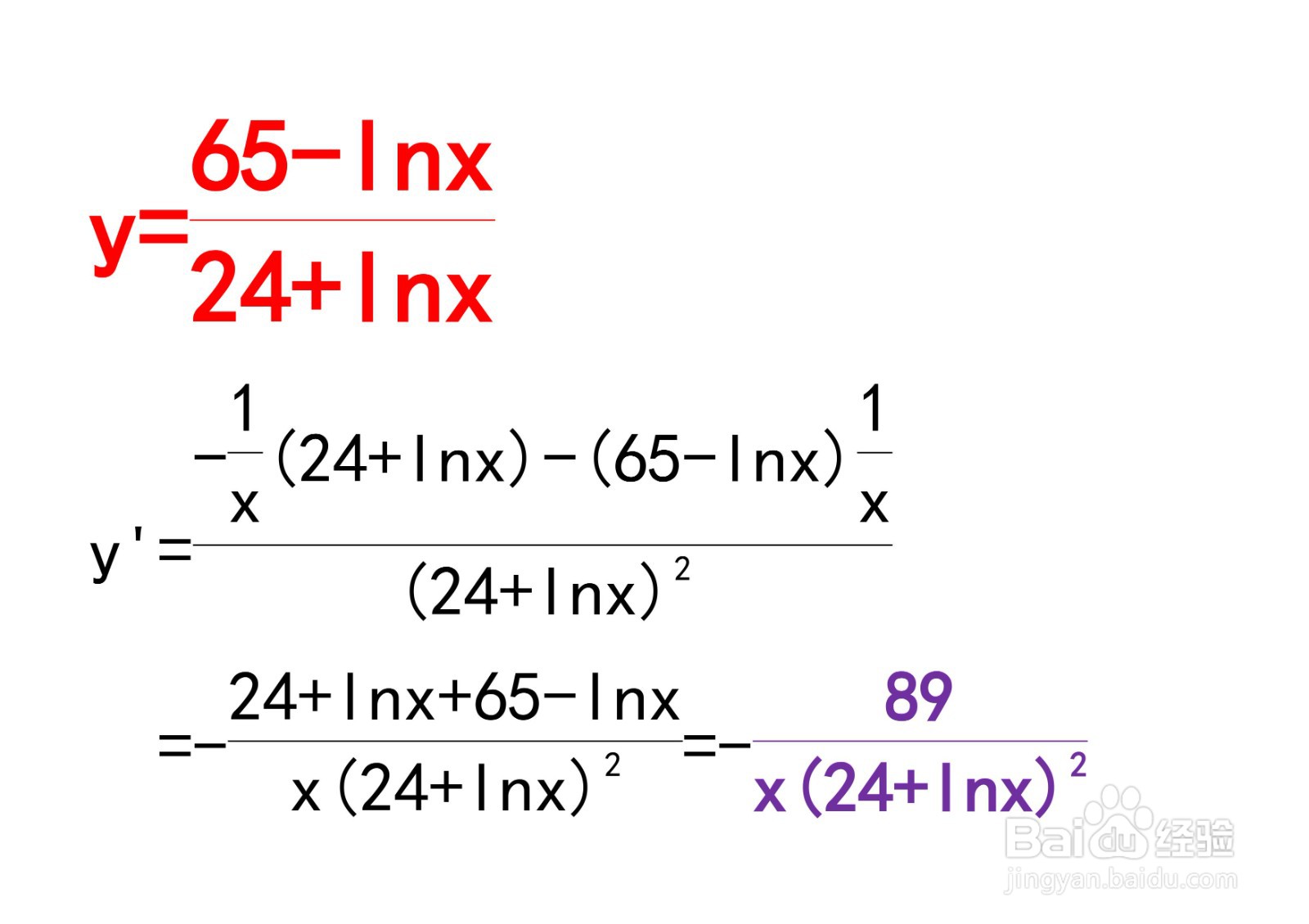
1、例题:函数y=cos(65-32x)导数计算步骤

思路：本题是正弦函数和一次函数的复合函数，主体为余弦函数，使用链式求导即可，过程如下：

y'=-sin(65-32x)(65-32x)'

  =32sin(65-32x)。

2、例题:函数y=5sinx-cos6x的导数计算   

思路：本题是正弦函数和余弦函数的和差函数，由和差函数的导数及三角函数的求导公式，即可计算，详细步骤如下。

y'=5cosx+sin6x.6=5cosx+6sin6x。

3、例题:函数y=sin45x6的导数计算

思路：本题是正弦函数与幂函数的复合函数，使用复合函数求导法则及正弦函数的导数公式计算即可。

y'=cos(45x^6)*(45x^6)'

=270*x^5*cos(45x^6)。

1、例题:函数y=xsin7x.ln8x的导数计算

思路：本题是幂函数、三角函数和对数函数的乘积，仍需使用函数乘积求导法则及相关函数的导数公式计算一阶导数。

y'=sin7x.ln8x+x(7cos7xln8x+sin7x/x)=sin7x.ln8x+sin7x+7xcos7x*ln8