怎么模拟圆盘里面的DLA模型？

1、画一个单位圆。

2、把DLA模型记为一组点的集合A，目前这个集合只有一个点，就是原点。

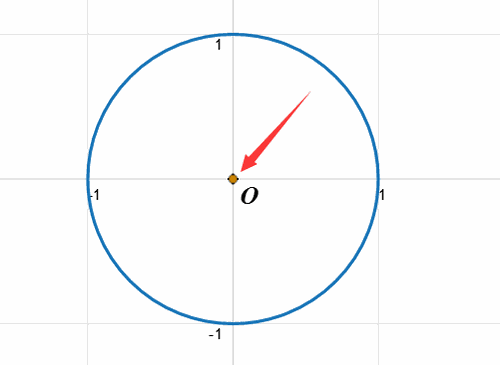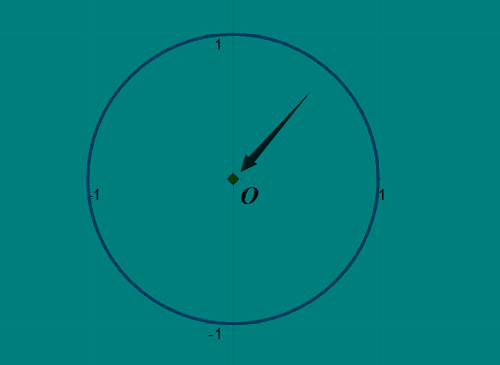
3、在圆上随机选择一个点，记为B。

这个点的选取方法很多，这里采用的方法是绘制极坐标点，极角是random(0, 2 * pi * m / m)，极径是1其中m是大于0的变量。

4、连接射线OB；

以O为圆心作半径为r的圆，其中r是介于0到0.01之间的实数；

这个圆与射线OB交于C。

现在，DLA模型点集A多了一个新成员——点C。

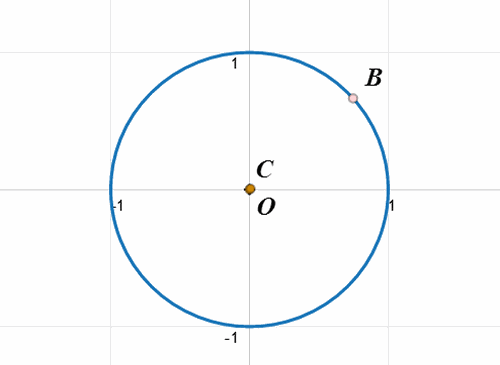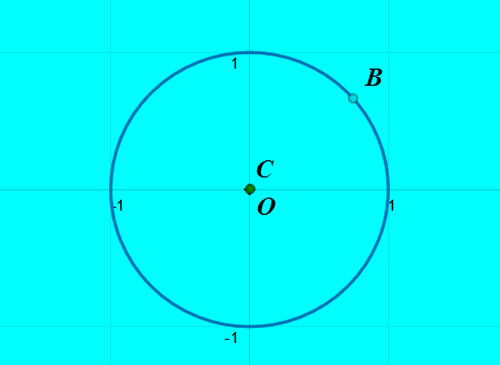
5、由于半径r太小，看起来C和O挤一起去了；

放大图形，可以发现，O和C之间还是有一定距离；

连接线段OC。

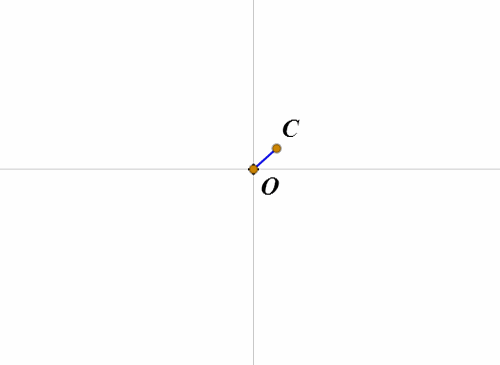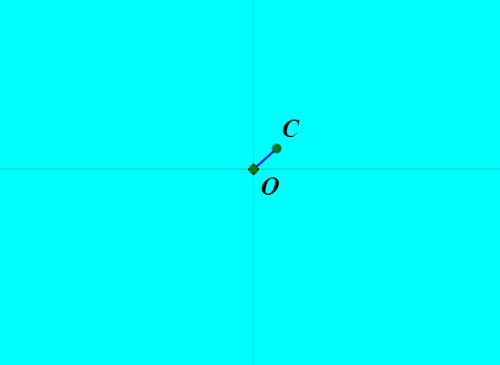
6、然后在单位圆上随机取第二个点，记为D；

从现在的点集A里面，找一个距离D最近的点x（如果O和C到D的距离相等，选择C为x）；

以x为圆心作半径为r的圆，作射线xD，圆与射线xD交于E。

但是，上述过程并不真正去作图，而是使用迭代来执行这个过程：

构造变量m；

计算m0=m+1；

进行迭代变换，O→B，m→m0，迭代深度为m。

由于网络画板目前难以实现最近点的寻找，所以这个课件搁浅了。

下图是一个假的DLA模型图。